Question

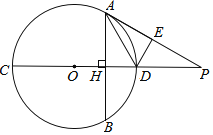
【题目】如图， 在⊙O 中，点 C 在优弧 AB 上， 将弧 BC 沿 BC 折叠后刚好经过 AB的中点 D． 若⊙O的半径为，AB=4，则 BC 的长是( )

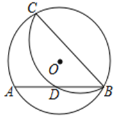
A.2B.3C.4D.2

Answer 1

【答案】B

【解析】

连接OD、AC、DC、OB、OC，作CE⊥AB于E，OF⊥CE于F，如图，利用垂径定理得到OD⊥AB，则AD=BD=AB=2，于是根据勾股定理可计算出OD=1，再利用折叠的性质可判断弧AC和弧CD所在的圆为等圆，则根据圆周角定理得到，所以AC=DC，利用等腰三角形的性质得AE=DE=1，接着证明四边形ODEF为正方形得到OF=EF=1，然后计算出CF后得到CE=BE=3，于是得到BC=3．

解：连接OD、AC、DC、OB、OC，作CE⊥AB于E，OF⊥CE于F，如图，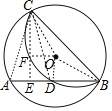

∵D为AB的中点，
∴OD⊥AB，
∴AD=BD=AB=2，

在Rt△OBD中，

∵将弧沿BC折叠后刚好经过AB的中点D．

∴弧AC和弧CD所在的圆为等圆，

∴AC=DC，
∴AE=DE=1，
∵CE⊥AB，OF⊥CE，OD⊥AB；AE=DE =OD=1

∴四边形ODEF为正方形，
∴OF=EF=1，
在Rt△OCF中，

∴CE=CF+EF=2+1=3，
∵BE=BD+DE=2+1=3，

故选：B．