Question

【题目】如图，已知点A(1，a)与点B(b，1)在反比例函数y＝(x＞0)图象上，点P(m，0)是x轴上的任意一点，若△PAB的面积为2，此时m的值是______．

Answer 1

【答案】﹣1或7

【解析】

把点A(1，a)与点B(b，1)代入反比例函数y＝(x＞0)，求出A,B坐标，延长AB交x轴于点C，如图2，设直线AB的解析式为y＝mx+n，求出点C的坐标，用割补法求出PC的值，结合点C的坐标即可.

解：∵点A(1，a)与点B(b，1)在反比例函数y＝(x＞0)图象上，

∴a＝2，b＝2，

∴点A(1，2)与点B(2，1)，

延长AB交x轴于点C，如图2，

设直线AB的解析式为y＝mx+n，

则有，

解得，

∴直线AB的解析式为y＝﹣x+3．

∵点C是直线y＝﹣x+3与x轴的交点，

∴点C的坐标为(3，0)，OC＝3，

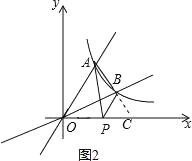
∵S△PAB＝2，

∴S△PAB＝S△PAC﹣S△PBC＝×PC×2﹣×PC×1＝PC＝2，

∴PC＝4．

∵C(3，0)，P(m，0)，

∴|m﹣3|＝4，

∴m＝﹣1或7，

故答案为：﹣1或7．