题目内容
（1997•昆明）如果一组数据x1，x2，x3，x4，x5的平均数是3，那么另一组数据x1-2，x2+2，x3+4，x4+6，x5-5的平均数是（ ）
分析：根据平均数的性质知，要求x1-2，x2+2，x3+4，x4+6，x5-5的平均数，只要把数x1、x2、x3、x4、x5的和表示出即可．
解答：解：∵数据x1、x2、x3、x4、x5的平均数为3，
∴数据x1+x2+x3+x4+x5=，3×5
∴x1-2，x2+2，x3+4，x4+6，x5-5的平均数为：
（x1-2+x2+2+x3+4+x4+6+x5-5）÷5
=（3×5+5）÷5
=4．
故选D．
∴数据x1+x2+x3+x4+x5=，3×5
∴x1-2，x2+2，x3+4，x4+6，x5-5的平均数为：
（x1-2+x2+2+x3+4+x4+6+x5-5）÷5
=（3×5+5）÷5
=4．
故选D．
点评：本题考查的是样本平均数的求法．解决本题的关键是用一组数据的平均数表示另一组数据的平均数．
练习册系列答案
相关题目
（1997•昆明）如图，?ABCD的对角线AC与BD相交于点O，E是CD的中点，AE交BD于F，则DF：FO=
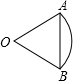
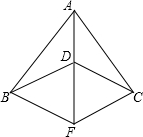（1997•昆明）已知：如图，AB=AC，DB=DC，F是AD的延长线上一点．求证：BF=CF．
（1997•昆明）已知：如图，AB是⊙O的直径，直线MN切⊙O于点C，AD⊥MN于D，AD交⊙O于E，AB的延长线交MN于点P．求证：AC2=AE•AP．