题目内容
(1997•昆明)如图,扇形OAB的面积为
πcm2,OA=OB,则弧AB的长=
π
πcm.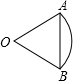
| 2 |
| 3 |
| 4 |
| 3 |
| 4 |
| 3 |

分析:因为OA=OB,OA=AB,所以三角形OAB是等边三角形,所以∠AOB=60°,再利用扇形的面积可求出圆的半径,利用弧长公式进而得到弧AB的长.
解答:解:∵OA=OB,OA=AB,
∴OA=OB=AB,
∴三角形OAB是等边三角形,
∴∠AOB=60°,
∵扇形OAB的面积为
π=
,
∴OA=2,
∴
=
=
π,
故答案为:=
π.
∴OA=OB=AB,
∴三角形OAB是等边三角形,
∴∠AOB=60°,
∵扇形OAB的面积为
| 2 |
| 3 |
| nπ(0A)2 |
| 360 |
∴OA=2,
∴
 |
| AB |
| 60•π•22 |
| 180 |
| 4 |
| 3 |
故答案为:=
| 4 |
| 3 |
点评:本题考查了扇形的面积公式和弧长公式的运用以及等边三角形的性质和判定,解题的关键是熟记各种计算公式.

练习册系列答案
相关题目
 (1997•昆明)如图,?ABCD的对角线AC与BD相交于点O,E是CD的中点,AE交BD于F,则DF:FO=
(1997•昆明)如图,?ABCD的对角线AC与BD相交于点O,E是CD的中点,AE交BD于F,则DF:FO= (1997•昆明)已知:如图,AB=AC,DB=DC,F是AD的延长线上一点.求证:BF=CF.
(1997•昆明)已知:如图,AB=AC,DB=DC,F是AD的延长线上一点.求证:BF=CF. (1997•昆明)已知:如图,AB是⊙O的直径,直线MN切⊙O于点C,AD⊥MN于D,AD交⊙O于E,AB的延长线交MN于点P.求证:AC2=AE•AP.
(1997•昆明)已知:如图,AB是⊙O的直径,直线MN切⊙O于点C,AD⊥MN于D,AD交⊙O于E,AB的延长线交MN于点P.求证:AC2=AE•AP.