题目内容
已知,如图,PA切⊙O于A,△ABC为⊙O的内接三角形,CA∥EP,AB、CB的延长线分别交DP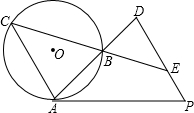 于点D、E.
于点D、E.
(1)求证:DE•DP=DA•DB.
(2)若AB=4,AC=6,DB=3,求DP的长.
(1)证明:∵CA∥EP,
∴∠C=∠DEB,∠D=∠CAD,
∵PA是⊙O的切线,
∴∠DAP=∠C,
∴∠DAP=∠DEB,
∴△BDE∽△PDA,
∴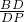 =
=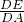 ,
,
∴DE•DP=DA•DB;
(2)解:∵CA∥EP,
∴△BDE∽△BAC,
则 =
= ,
,
∵AB=4,AC=6,DB=3,
∴DE= ,
,
∵DE•DP=DA•DB,
∴DP=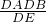 =
=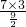 =
= .
.
分析:(1)根据题意可证得△BDE∽△PDA,从而得出DE•DP=DA•DB;
(2)可证得△BDE∽△BAC,则 =
= ,从而求得DE,
,从而求得DE,
点评:本题是一道和圆有关的题目,考查了相似三角形的判定和性质,以及切线的性质,是中考压轴题,难度较大.
∴∠C=∠DEB,∠D=∠CAD,
∵PA是⊙O的切线,
∴∠DAP=∠C,
∴∠DAP=∠DEB,
∴△BDE∽△PDA,
∴
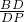 =
=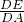 ,
,∴DE•DP=DA•DB;
(2)解:∵CA∥EP,
∴△BDE∽△BAC,
则
 =
= ,
,∵AB=4,AC=6,DB=3,
∴DE=
 ,
,∵DE•DP=DA•DB,
∴DP=
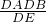 =
= =
= .
.分析:(1)根据题意可证得△BDE∽△PDA,从而得出DE•DP=DA•DB;
(2)可证得△BDE∽△BAC,则
 =
= ,从而求得DE,
,从而求得DE,点评:本题是一道和圆有关的题目,考查了相似三角形的判定和性质,以及切线的性质,是中考压轴题,难度较大.

练习册系列答案
 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案 小学期末标准试卷系列答案
小学期末标准试卷系列答案
相关题目
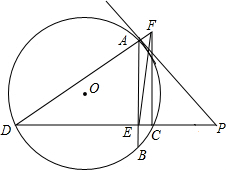 已知,如图,PA切⊙O于点A,割线PD交⊙O于点C、D,∠P=45°,弦AB⊥PD,垂足为E,且BE=2CE,DE=6,CF⊥PC,交DA的延长线于点F.求tan∠CFE的值.
已知,如图,PA切⊙O于点A,割线PD交⊙O于点C、D,∠P=45°,弦AB⊥PD,垂足为E,且BE=2CE,DE=6,CF⊥PC,交DA的延长线于点F.求tan∠CFE的值. 已知:如图,PA切⊙O于点A,割线PBC交⊙O于点B、C,PD⊥AB于点D,PD、AO的延长线相交于点E,连接CE并延长CE交⊙O于点F,连接AF.
已知:如图,PA切⊙O于点A,割线PBC交⊙O于点B、C,PD⊥AB于点D,PD、AO的延长线相交于点E,连接CE并延长CE交⊙O于点F,连接AF. 于点D、E.
于点D、E. 已知:如图,PA切⊙O于A点,PO∥AC,BC是⊙O的直径.请问:直线PB是否与⊙O相切?说明你的理由.
已知:如图,PA切⊙O于A点,PO∥AC,BC是⊙O的直径.请问:直线PB是否与⊙O相切?说明你的理由. 已知:如图,PA切⊙O于A点,PO交⊙O于B点.PA=15cm,PB=9cm.求⊙O的半径长.
已知:如图,PA切⊙O于A点,PO交⊙O于B点.PA=15cm,PB=9cm.求⊙O的半径长.