Question

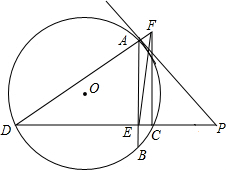
已知：如图，PA切⊙O于点A，割线PBC交⊙O于点B、C，PD⊥AB于点D，PD、AO的延长线相交于点E，连接CE并延长CE交⊙O于点F，连接AF．
（1）求证：△PBD∽△PEC；
（2）若AB=12，tan∠EAF=

2

3

，求⊙O半径的长．

Answer 1

分析：（1）欲证两三角形相似，在此题所给的已知条件中，可运用两组边对应成比例，且夹角相等来证明，∠APE的余弦值在△APD和△APE中，有两种表示方法，从而得出一个等积式，根据切割线定理，再得到一个等积式，从而借助于PA²得到对应线段成比例，进而解答；
（2）由（1）得∠C=90°，所以BF是直径，得∠BAF=90°，作OH⊥AB于H点，则∠HOA=∠EAF，在△HOA中求半径OA的长．

解答：（1）证明：∵PA切⊙O于点A，
∴AO⊥PA．
∵PD⊥AB，
∴

PA

PE

=cos∠APE=

PD

PA

．
∴PA²=PD•PE…①
∵PBC是⊙O的割线，PA为⊙O切线，
∴PA²=PB•PC…②
联立①②，得PD•PE=PB•PC，
即

PB

PD

=

PE

PC

．
又∠BPD=∠EPC，
∴△PBD∽△PEC．

（2）解：连接BF，作OH⊥AB于H点，
∵△PBD∽△PEC，
∴∠C=∠PDB=90°．
∴BF是直径．
∴∠BAF=90°．
∵OH⊥AB，
∴OH∥AF．
∴∠EAF=∠HOA．
∴tan∠EAF=tan∠HOA=AH：OH=2：3．
又AB=12，
∴AH=6．
∴OH=9．
∴OA=

62+92

=3

13

．

点评：此题考查了三角函数、切割线定理，以及相似的判定，比较全面，难易程度适中．