题目内容
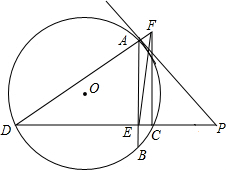 已知,如图,PA切⊙O于点A,割线PD交⊙O于点C、D,∠P=45°,弦AB⊥PD,垂足为E,且BE=2CE,DE=6,CF⊥PC,交DA的延长线于点F.求tan∠CFE的值.
已知,如图,PA切⊙O于点A,割线PD交⊙O于点C、D,∠P=45°,弦AB⊥PD,垂足为E,且BE=2CE,DE=6,CF⊥PC,交DA的延长线于点F.求tan∠CFE的值.
分析:求tan∠CFE的值就要找垂直关系,用边表示出来,转化为求边长的问题,由已知条件CF⊥PC,可以推出tan∠CFE=
,再利用圆的性质和切线的性质求出CE和FC两边的长度即可.
| CE |
| FC |
解答:解:由相交弦定理,得AE•BE=DE•CE
又∵BE=2CE
∴AE•2CE=6CE
∴AE=3
∵AB⊥PD
∴∠AEP=90°
又∵∠P=45°
∴∠EAP=∠P=45°
∴PE=AE=3
在Rt△AEP中,由勾股定理,得:
PA=
=
=3
∵PA切⊙O于点A
∴PA2=PC•PD
∴PC=
=
=2
∴CE=PE-PC=3-2=1
∵FC⊥PD∴∠FCE=90°
又∵∠AED=90°
∴∠AED=∠FCE
∴AE∥FC
∴
=
∴FC=
=
=
∴tan∠CFE=
=
=
.
又∵BE=2CE
∴AE•2CE=6CE
∴AE=3
∵AB⊥PD
∴∠AEP=90°
又∵∠P=45°
∴∠EAP=∠P=45°
∴PE=AE=3
在Rt△AEP中,由勾股定理,得:
PA=
| AE2+PE2 |
| 32+32 |
| 2 |
∵PA切⊙O于点A
∴PA2=PC•PD
∴PC=
| PA2 |
| PO |
(3
| ||
| 3+6 |
∴CE=PE-PC=3-2=1
∵FC⊥PD∴∠FCE=90°
又∵∠AED=90°
∴∠AED=∠FCE
∴AE∥FC
∴
| DE |
| DC |
| AE |
| FC |
∴FC=
| DC•AE |
| DE |
| (6+1)×3 |
| 6 |
| 7 |
| 2 |
∴tan∠CFE=
| CE |
| FC |
| 1 | ||
|
| 2 |
| 7 |
点评:此题考查知识点较多,有圆的性质,平行线分线段成比例,相交弦定理,勾股定理及切割线定理,是一道综合性较强的题,同时也用到转化思想,把求tan∠CFE的问题转化为求边长的问题.

练习册系列答案
相关题目
 已知:如图,PA切⊙O于点A,割线PBC交⊙O于点B、C,PD⊥AB于点D,PD、AO的延长线相交于点E,连接CE并延长CE交⊙O于点F,连接AF.
已知:如图,PA切⊙O于点A,割线PBC交⊙O于点B、C,PD⊥AB于点D,PD、AO的延长线相交于点E,连接CE并延长CE交⊙O于点F,连接AF. 于点D、E.
于点D、E. 已知:如图,PA切⊙O于A点,PO∥AC,BC是⊙O的直径.请问:直线PB是否与⊙O相切?说明你的理由.
已知:如图,PA切⊙O于A点,PO∥AC,BC是⊙O的直径.请问:直线PB是否与⊙O相切?说明你的理由. 已知:如图,PA切⊙O于A点,PO交⊙O于B点.PA=15cm,PB=9cm.求⊙O的半径长.
已知:如图,PA切⊙O于A点,PO交⊙O于B点.PA=15cm,PB=9cm.求⊙O的半径长.