题目内容
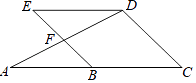
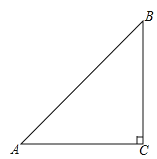
【题目】如图,已知Rt△ACB中,∠C=90°,∠BAC=45°.
(1)(4分)用尺规作图,在CA的延长线上截取AD=AB,并连接BD(不写作法,保留作图痕迹);
(2)(4分)求∠BDC的度数;
(3)(4分)定义:在直角三角形中,一个锐角A的邻边与对边的比叫做∠A的余切,记作cotA,即![]() ,根据定义,利用图形求cot22.5°的值.
,根据定义,利用图形求cot22.5°的值.
【答案】(1)答案见试题解析;(2)22.5°;(3)![]() .
.
【解析】
试题分析:(1)以点A为圆心,AB为半径作弧交CA的延长线于D,然后连结BD;
(2)由AD=AB得∠ADB=∠ABD,然后利用三角形外角性质可求出∠ADB=22.5°;
(3)设AC=x,根据题意得△ACB为等腰直角三角形,则BC=AC=x,AB=![]() ,所以AD=AB=
,所以AD=AB=![]() ,CD=
,CD=![]() ,在Rt△BCD中,根据余切的定义求解.
,在Rt△BCD中,根据余切的定义求解.
试题解析:(1)如图,

(2)∵AD=AB,∴∠ADB=∠ABD,而∠BAC=∠ADB+∠ABD,∴∠ADB=![]() ∠BAC=
∠BAC=![]() ×45°=22.5°,即∠BDC的度数为22.5°;
×45°=22.5°,即∠BDC的度数为22.5°;
(3)设AC=x,∵∠C=90°,∠BAC=45°,∴△ACB为等腰直角三角形,∴BC=AC=x,AB=![]() AC=
AC=![]() ,∴AD=AB=
,∴AD=AB=![]() ,∴CD=
,∴CD=![]() =
=![]() ,在Rt△BCD中,cot∠BDC=
,在Rt△BCD中,cot∠BDC=![]() =
=![]() =
=![]() ,即cot22.5°=
,即cot22.5°=![]() .
.

练习册系列答案
 互动英语系列答案
互动英语系列答案
相关题目