题目内容
【题目】如图，将一张正方形纸片，第1次剪成四个大小形状一样的小正方形，第2次将其中的一个小正方形再按同样的方法剪成四个小正方形，然后再将其中的一个小正方形剪成四个小正方形，如此循环进行下去，如果共剪
次，则可剪出 个正方形.
【答案】3n+1
【解析】根据题意可以发现：每一次剪的时候，都是把上一次的图形中的一个进行剪．所以在4的基础上，依次多3个，继而解答各题即可．
解：根据题意可知：后一个图形中的个数总比前一个图形中的个数多3个，
即剪第1次时，可剪出4个正方形；
剪第2次时，可剪出7个正方形；
剪第3次时，可剪出10个正方形；
剪第4次时，可剪出13个正方形；
…
剪n次时，共剪出小正方形的个数为：4+3（n-1）=3n+1．
故答案为：3n+1．
本题考查剪纸问题，同时考查规律型中的图形变化问题，同时考查学生观察、分析、归纳和应用规律的能力．
练习册系列答案
阅读快车系列答案
相关题目
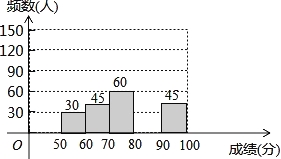
【题目】(2016湖北省荆州市第20题)为了弘扬荆州优秀传统文化，某中学举办了荆州文化知识大赛，其规则是：每位参赛选手回答100道选择题，答对一题得1分，不答或错答为得分、不扣分，赛后对全体参赛选手的答题情况进行了相关统计，整理并绘制成如下图表：
组别 | 分数段 | 频数（人） | 频率 |
1 | 50≤x＜60 | 30 | 0.1 |
2 | 60≤x＜70 | 45 | 0.15 |
3 | 70≤x＜80 | 60 | n |
4 | 80≤x＜90 | m | 0.4 |
5 | 90≤x＜100 | 45 | 0.15 |
请根据以图表信息，解答下列问题：
（1）表中m= ，n= ；
（2）补全频数分布直方图；
（3）全体参赛选手成绩的中位数落在第几组；
（4）若得分在80分以上（含80分）的选手可获奖，记者从所有参赛选手中随机采访1人，求这名选手恰好是获奖者的概率．
