题目内容
【题目】若∠A与∠B的两边分别垂直,请判断这两个角的等量关系.
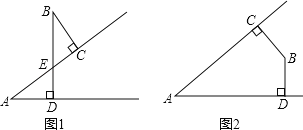
(1)如图1,∠A与∠B的关系是 ;如图2,∠A与∠B的关系是 ;
(2)若∠A与∠B的两边分别平行,试探索这两个角的等量关系,画图并证明你的结论.
【答案】(1)∠A=∠B,∠A+∠B=180°;(2)见解析
【解析】
试题分析:(1)根据垂直的量相等的角都等于90°,对顶角相等,所以∠A=∠B,同样根据垂直的量相等的角都等于90°,根据四边形的内角和等于360°,所以∠A+∠B=360°﹣90°﹣90°=180°.所以如果一个角的两边与另一个角的两边分别垂直,那么这两个角的关系是相等或互补;
(2)根据平行线的性质得到同位角相等,同旁内角互补即可得到结论.
(1)如图1,∠A=∠B,
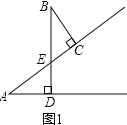
∵∠ADE=∠BCE=90°,∠AED=∠BEC,
∴∠A=180°﹣∠ADE﹣∠AED,
∠B=180°﹣∠BCE﹣∠BEC,
∴∠A=∠B,
如图2,∠A+∠B=180°;
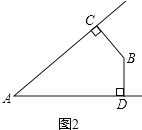
∴∠A+∠B=360°﹣90°﹣90°=180°.
∴∠A与∠B的等量关系是互补;
故答案为:∠A=∠B,∠A+∠B=180°;
(2)如图3,∠A=∠B,
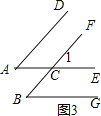
∵AD∥BF,∴∠A=∠1,
∵AE∥BG,∴∠1=∠B,
∴∠A=∠B;
如图4,∠A+∠B=180°,
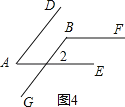
∵AD∥BG,
∴∠A=∠2,
∵AE∥BF,
∴∠2+∠B=180°,
∴∠A+∠B=180°.

练习册系列答案
 全优点练单元计划系列答案
全优点练单元计划系列答案
相关题目

