题目内容
【题目】在平面直角坐标系中有两点A(-2,2),B(1,4),根据要求求出P点的坐标:
(1)在x轴上找一点P,使得![]() 最小
最小
(2)在y轴上找一点P,使得![]() 最小
最小
(3)在x轴上找一点P,使得![]() 最大
最大
(4)在x轴上找一点P,使得![]() 最小
最小
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() ;(4)
;(4)![]()
【解析】
试题分析:
(1)由于两点间线段最短,故作A关于x轴的对称点A’,连接A’B与x轴相交于点P,
则点P即为试PA+PB最短的点
(2)由于两点间线段最短,故连接AB交y轴于P,则点P即为使PA+PB最短的点
(3)连接BA并延长交x轴于P,则点P即为使![]() 最大的点
最大的点
(4)因为![]() ,所以当
,所以当![]() ,时
,时![]() 最小,即点
最小,即点![]() 最小在
最小在![]() 最小的垂直平分线上
最小的垂直平分线上
试题解析:
解:(1)如下图,作A关于x轴的对称点A’,连接A’B与x轴相交于点P,
则点P即为试PA+PB最短的点
∵A(-2,2)
∴A’(-2,-2)
设直线A’B的解析式为:![]()
∴![]()
∴![]()
∴直线A’B的解析式为:![]()
当![]() 时,
时,![]()
∴![]()

(2)如下图,连接AB交y轴于P,则点P即为使PA+PB最短的点
设直线AB的解析式为:![]()
∴![]()
∴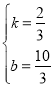
∴直线A’B的解析式为:![]()
当![]() 时,
时,![]()
∴![]()
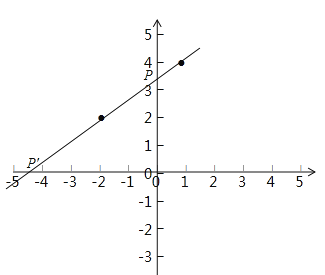
(3)连接BA并延长交x轴于![]() ,则点
,则点![]() 即为使
即为使![]() 最大的点
最大的点
由(2)得直线AB的解析式为:![]()
当y=0时,![]()
∴![]()
(4)如图,∵![]() ,
,
∴当AP=BP时,![]() 最小
最小
故点P在线段AB的垂直平分线上,作线段AB的垂直平分线交x轴于点P,
则点P即为所求
设P(x,0),则PA’=PB
即![]()
解得:![]()
故点P的坐标为![]()


练习册系列答案
 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案
相关题目