题目内容
老师要求同学们在图①中 内找一点P,使点P到OM、ON的距离相等.
内找一点P,使点P到OM、ON的距离相等.
小明是这样做的:在OM、ON上分别截取OA=OB,连结AB,取AB中点P,点P即为所求.
请你在图②中的 内找一点P,使点P到OM的距离是到ON距离的2倍.要求:简单叙述做法,并对你的做法给予证明.
内找一点P,使点P到OM的距离是到ON距离的2倍.要求:简单叙述做法,并对你的做法给予证明.
作法见解析;证明见解析.
解析试题分析:在OM、ON上分别截取OA=OB,连结AB.在∠MAB内做射线AH,并在AH上顺次截取AC=CD=DG,连结BG.分别过C、D两点做DP∥BG、CQ∥BG.点P即为所求.
试题解析:做法:
(1)在OM、ON上分别截取OA=OB,连结AB.
(2)在∠MAB内做射线AH,并在AH上顺次截取AC=CD=DG,连结BG.
(3)分别过C、D两点做DP∥BG、CQ∥BG.
点P即为所求.
证明:作 ,
, ,垂足分别为E、F.
,垂足分别为E、F.
则有 .
.
∵OA=OB,∴
∴  ∽
∽
∴
∴ 点P即为所求.
考点: (1)几何作图;(2)相似三角形的判定与性质.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
 ,猜想EF与DE的位置关系,并说明理由.
,猜想EF与DE的位置关系,并说明理由.
 ,求
,求 的值.
的值. 
 ,那么
,那么
 ,那么
,那么 的值为 (用含m,n的代数式表示).
的值为 (用含m,n的代数式表示).
 ,求代数式
,求代数式 的值.
的值.
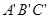 是以坐标原点O为位似中心的位似图形,且点B(3,1),B′(6,2).
是以坐标原点O为位似中心的位似图形,且点B(3,1),B′(6,2).
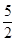 ,3),则A′的坐标为 ;②△ABC与△
,3),则A′的坐标为 ;②△ABC与△
 m,两楼的高各为10m和30m,则当你至少与M楼相距多少m时,才能看到后面的N楼?
m,两楼的高各为10m和30m,则当你至少与M楼相距多少m时,才能看到后面的N楼?
