题目内容
探索研究已知二次函数y=x2+bx+c中,函数y与自变量x的部分对应值如下表:
| x | … | -1 | 1 | 2 | 3 | … | |
| y | … | -5 | -8 | -9 | -8 | … |
(2)若A(m,y1),B(m+4,y2)两点都在该函数的图象上.
①试比较y1与y2的大小;
②若A、B两点位于x轴的下方,点P为函数图象的对称轴与x轴的交点,点Q为函数图象上的一点,解答以下问题:
(Ⅰ)直接写出实数m的变化范围是______;
(Ⅱ)是否存在实数m,使得四边形APBQ为平行四边形?若存在,请求出m的值,并写出点Q的坐标;若不存在,请说明理由.
【答案】分析:(1)任取两点坐标,利用待定系数法求函数解析式,根据表格中提供的数据画出图象;
(2)①求出y1-y2的表达式,然再分大于0,等于0,小于0三种情况讨论;
②(Ⅰ)先求出二次函数图象与x轴的交点的横坐标,再根据交点在x轴的下方,令m大于左边点的横坐标,m+4小于右边点的横坐标,解不等式即可;
(Ⅱ)先求出AB与x轴平行,所以分(i)AB为平行四边形的边时,PQ与AB平行,此时点Q就是二次函数与x轴的交点,(ii)AB为平行四边形的对角线,根据平行四边形的对角线互相平分的性质,PQ平分AB,所以点Q就是二次函数的顶点,然后分别讨论求解.
解答: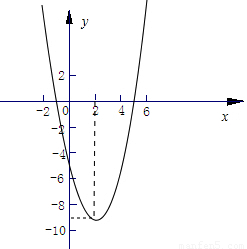 解:(1)根据题意,
解:(1)根据题意, ,
,
解得 ,
,
∴该二次函数解析式为y=x2-4x-5,图象如右;
(2)①y1-y2=m2-4m-5-(m+4)2+4(m+4)+5=-8m,
∴当m>0时,-8m<0,y1<y2,
当m=0时,-8m=0,y1=y2,
当m<0时,-8m>0,y1>y2;
②(Ⅰ)当y=0时,x2-4x-5=0,
解得x1=-1,x2=5,
∴二次函数与x轴的交点坐标为(-1,0),(5,0),
∵A、B两点位于x轴的下方,
∴m>-1,m+4<5,
解得-1<m<1;
(Ⅱ)∵二次函数对称轴为x=-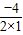 =2,
=2,
AB=| |=2,
|=2,
∴点A、B关于对称轴对称,
∴AB∥x轴,
(i)若AB为平行四边形的边,则PQ∥AB,
∴点Q为二次函数图象与x轴的交点,此时PQ=2-(-1)=3,或PQ=5-2=3,
而AB=m+4-m=4,
AB≠PQ,
∴AB不能是平行四边形的边;
(ii)若AB为平行四边形的对角线,根据AB关于对称轴对称,得
点Q为二次函数顶点,
又x=2时,y=22-4×2-5=-9,
∴点Q坐标是(2,-9),
根据平行四边形对角线互相平分,点A、B的纵坐标是 =-4.5,
=-4.5,
此时,m2-4m-5=-4.5,
解得m= ,或m=
,或m=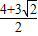 (舍去).
(舍去).
又∵此时AB∥x轴,
∴y1=y2,
∴-8m=0,
解得m=0,
∵m= ≠0,
≠0,
∴不存在实数m,使得四边形APBQ为平行四边形.
点评:本题是二次函数的综合题型,其中涉及的知识点有待定系数法求函数解析式,两点的距离公式,平行四边形的性质,解一元二次方程,综合性较强,难度较大.
(2)①求出y1-y2的表达式,然再分大于0,等于0,小于0三种情况讨论;
②(Ⅰ)先求出二次函数图象与x轴的交点的横坐标,再根据交点在x轴的下方,令m大于左边点的横坐标,m+4小于右边点的横坐标,解不等式即可;
(Ⅱ)先求出AB与x轴平行,所以分(i)AB为平行四边形的边时,PQ与AB平行,此时点Q就是二次函数与x轴的交点,(ii)AB为平行四边形的对角线,根据平行四边形的对角线互相平分的性质,PQ平分AB,所以点Q就是二次函数的顶点,然后分别讨论求解.
解答:
 解:(1)根据题意,
解:(1)根据题意, ,
,解得
 ,
,∴该二次函数解析式为y=x2-4x-5,图象如右;
(2)①y1-y2=m2-4m-5-(m+4)2+4(m+4)+5=-8m,
∴当m>0时,-8m<0,y1<y2,
当m=0时,-8m=0,y1=y2,
当m<0时,-8m>0,y1>y2;
②(Ⅰ)当y=0时,x2-4x-5=0,
解得x1=-1,x2=5,
∴二次函数与x轴的交点坐标为(-1,0),(5,0),
∵A、B两点位于x轴的下方,
∴m>-1,m+4<5,
解得-1<m<1;
(Ⅱ)∵二次函数对称轴为x=-
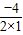 =2,
=2,AB=|
 |=2,
|=2,∴点A、B关于对称轴对称,
∴AB∥x轴,
(i)若AB为平行四边形的边,则PQ∥AB,
∴点Q为二次函数图象与x轴的交点,此时PQ=2-(-1)=3,或PQ=5-2=3,
而AB=m+4-m=4,
AB≠PQ,
∴AB不能是平行四边形的边;
(ii)若AB为平行四边形的对角线,根据AB关于对称轴对称,得
点Q为二次函数顶点,
又x=2时,y=22-4×2-5=-9,
∴点Q坐标是(2,-9),
根据平行四边形对角线互相平分,点A、B的纵坐标是
 =-4.5,
=-4.5,此时,m2-4m-5=-4.5,
解得m=
 ,或m=
,或m=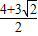 (舍去).
(舍去).又∵此时AB∥x轴,
∴y1=y2,
∴-8m=0,
解得m=0,
∵m=
 ≠0,
≠0,∴不存在实数m,使得四边形APBQ为平行四边形.
点评:本题是二次函数的综合题型,其中涉及的知识点有待定系数法求函数解析式,两点的距离公式,平行四边形的性质,解一元二次方程,综合性较强,难度较大.

练习册系列答案
相关题目
 探索研究
探索研究已知二次函数y=x2+bx+c中,函数y与自变量x的部分对应值如下表:
| x | … | -1 | 0 | 1 | 2 | 3 | … |
| y | … | 0 | -5 | -8 | -9 | -8 | … |
(2)若A(m,y1),B(m+4,y2)两点都在该函数的图象上.
①试比较y1与y2的大小;
②若A、B两点位于x轴的下方,点P为函数图象的对称轴与x轴的交点,点Q为函数图象上的一点,解答以下问题:
(Ⅰ)直接写出实数m的变化范围是
(Ⅱ)是否存在实数m,使得四边形APBQ为平行四边形?若存在,请求出m的值,并写出点Q的坐标;若不存在,请说明理由.
 探索研究
探索研究
已知二次函数y=x2+bx+c中,函数y与自变量x的部分对应值如下表:
| x | … | -1 | 0 | 1 | 2 | 3 | … |
| y | … | 0 | -5 | -8 | -9 | -8 | … |
(2)若A(m,y1),B(m+4,y2)两点都在该函数的图象上.
①试比较y1与y2的大小;
②若A、B两点位于x轴的下方,点P为函数图象的对称轴与x轴的交点,点Q为函数图象上的一点,解答以下问题:
(Ⅰ)直接写出实数m的变化范围是______;
(Ⅱ)是否存在实数m,使得四边形APBQ为平行四边形?若存在,请求出m的值,并写出点Q的坐标;若不存在,请说明理由.
 问题情境
问题情境 (2012•营口一模)[提出问题]:已知矩形的面积为1,当该矩形的长为多少时,它的周长最小?最小值是多少?
(2012•营口一模)[提出问题]:已知矩形的面积为1,当该矩形的长为多少时,它的周长最小?最小值是多少?