��Ŀ����
 �����龳
�����龳��֪���ε����Ϊa��aΪ������a��0�������þ��εij�Ϊ����ʱ�������ܳ���С����Сֵ�Ƕ��٣�
��ѧģ��
��þ��εij�Ϊx���ܳ�Ϊy����y��x�ĺ�����ϵʽΪy=2(x+
| a |
| x |
̽���о�
��1�����ǿ��Խ��ѧϰ�����ľ��飬��̽������y=x+
| 1 |
| x |
1��д�±�������������ͼ��
| x | �� |
|
|
|
1 | 2 | 3 | 4 | �� | ||||||
| y | �� | �� |
��������κ���y=ax2+bx+c��a��0�������С��ֵʱ������ͨ���۲�ͼ����ͨ���۲�ͼ������ͨ���䷽�õ���ͬ��ͨ���䷽Ҳ��������y=x+
| 1 |
| x |
| 1 |
| x |
| x |
|
| x |
|
| x |
|
| x |
|
=(
| x |
|
��
| x |
|
| 1 |
| x |
�������
��2������������龳���е����⣬ֱ��д���𰸣�
��������1���ٸ��������ʽ��ֵ�ķ�����x��ֵ�����Ľ���ʽ�����ֵ�Ϳ����ˣ�
�ڸ��ݢٱ��е����ݻ���������ͼ���ٽ�ϱ��е����ݾͿ���д��ͼ�����Ӧ�����ʣ�
��2���ɢ۵Ľ��ۿ���x=
ֱ�Ӵ���y��x�ĺ�����ϵʽΪy=2(x+
)(x��0)�Ϳ�������ܳ�����Сֵ��
�ڸ��ݢٱ��е����ݻ���������ͼ���ٽ�ϱ��е����ݾͿ���д��ͼ�����Ӧ�����ʣ�
��2���ɢ۵Ľ��ۿ���x=
| a |
| a |
| x |
����⣺��1���ٵ�x=
ʱ��y=
��
��x=
ʱ��y=
��
��x=
ʱ��y=
��
��x=1��2��3��4��ʱ����yֵ�ֱ�Ϊ��2��
��
��
��
�ຯ��y=x+
��x��0����ͼ����ͼ��

�ڵ�0��x��1ʱ��y��x�������С����x��1ʱ��y��x���������x=1ʱ����y=x+
��x��0������СֵΪ2��
��2���ɢ۵ã����þ��εij�Ϊ
ʱ��
�����ܳ���С����СֵΪy=2(
+
)=4
��
| 1 |
| 4 |
| 17 |
| 4 |
��x=
| 1 |
| 3 |
| 10 |
| 3 |
��x=
| 1 |
| 2 |
| 5 |
| 2 |
��x=1��2��3��4��ʱ����yֵ�ֱ�Ϊ��2��
| 5 |
| 2 |
| 10 |
| 3 |
| 17 |
| 4 |
�ຯ��y=x+
| 1 |
| x |

�ڵ�0��x��1ʱ��y��x�������С����x��1ʱ��y��x���������x=1ʱ����y=x+
| 1 |
| x |
��2���ɢ۵ã����þ��εij�Ϊ
| a |
�����ܳ���С����СֵΪy=2(
| a |
| a | ||
|
| a |
������������һ�����κ������ۺ����⣬��������㷨��������ͼ��ķ��������κ�����ֵ�����ã�������������ͼ�����ʵ����ã�

��ϰ��ϵ�д�
�����Ŀ
����������12�֣�
�����龳
��֪���ε����Ϊa��aΪ������a��0�������þ��εij�Ϊ����ʱ�������ܳ���С����Сֵ�Ƕ��٣�
��ѧģ��
��þ��εij�Ϊx���ܳ�Ϊy����y��x�ĺ�����ϵʽΪ![]() ��
��
̽���о�
�����ǿ��Խ����ǰ�о������ľ��飬��̽������![]() ��ͼ�����ʣ�
��ͼ�����ʣ�
�� ��д�±�������������ͼ��
| x | �� |
|
|
| 1 | 2 | 3 | 4 | �� |
| y | �� |
|
|
|
|
|
|
| �� |
�ڹ۲�ͼ��д���ú���������ͬ���͵����ʣ�
��������κ���y=ax2��bx��c��a��0�������С��ֵʱ������ͨ���۲�ͼ������ͨ���䷽�õ�������ͨ���䷽����![]() (x��0)����Сֵ��
(x��0)����Сֵ��
�������
����������������������龳���е����⣬ֱ��д���𰸣�
����������12�֣�
�����龳
��֪���ε����Ϊa��aΪ������a��0�������þ��εij�Ϊ����ʱ�������ܳ���С����Сֵ�Ƕ��٣�
��ѧģ��
��þ��εij�Ϊx���ܳ�Ϊy����y��x�ĺ�����ϵʽΪ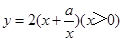 ��
��
̽���о�
�����ǿ��Խ����ǰ�о������ľ��飬��̽������ ��ͼ�����ʣ�
��ͼ�����ʣ�
�� ��д�±�������������ͼ��
�ڹ۲�ͼ��д���ú���������ͬ���͵����ʣ�
��������κ���y=ax2��bx��c��a��0�������С��ֵʱ������ͨ���۲�ͼ������ͨ���䷽�õ�������ͨ���䷽����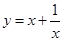 (x��0)����Сֵ��
(x��0)����Сֵ��
�������
����������������������龳���е����⣬ֱ��д���𰸣�
�����龳
��֪���ε����Ϊa��aΪ������a��0�������þ��εij�Ϊ����ʱ�������ܳ���С����Сֵ�Ƕ��٣�
��ѧģ��
��þ��εij�Ϊx���ܳ�Ϊy����y��x�ĺ�����ϵʽΪ
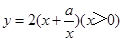 ��
��̽���о�
�����ǿ��Խ����ǰ�о������ľ��飬��̽������
 ��ͼ�����ʣ�
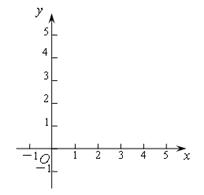
��ͼ�����ʣ��� ��д�±�������������ͼ��
| x | �� | 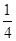 |  | 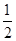 | 1 | 2 | 3 | 4 | �� |
| y | �� | | | | | | | | �� |
��������κ���y=ax2��bx��c��a��0�������С��ֵʱ������ͨ���۲�ͼ������ͨ���䷽�õ�������ͨ���䷽����
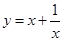 (x��0)����Сֵ��
(x��0)����Сֵ���������
����������������������龳���е����⣬ֱ��д���𰸣�

������10�֣������龳
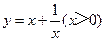
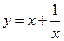
��֪���ε����Ϊa��aΪ������a��0�������þ��εij�Ϊ����ʱ�������ܳ���С����Сֵ�Ƕ��٣�
��ѧģ��
��þ��ε�һ�߳�Ϊx���ܳ�Ϊy����y��x�ĺ�����ϵʽΪ ��
̽���о�
�����ǿ��Խ����ǰ�о������ľ��飬��̽��������ͼ�����ʣ�
����д�±�������������ͼ��
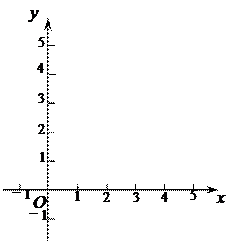
�ڹ۲�ͼ���������ú�����������(y��x�仯����ʲô�仯������������κ���y=ax��bx��c��a��0�������С��ֵʱ������ͨ���۲�ͼ������ͨ��
�䷽�õ�������ͨ���䷽����(x��0)����Сֵ��
�������
����������������������龳���е����⣬ֱ��д���𰸣�
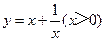
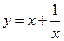
��֪���ε����Ϊa��aΪ������a��0�������þ��εij�Ϊ����ʱ�������ܳ���С����Сֵ�Ƕ��٣�
��ѧģ��
��þ��ε�һ�߳�Ϊx���ܳ�Ϊy����y��x�ĺ�����ϵʽΪ ��
̽���о�
�����ǿ��Խ����ǰ�о������ľ��飬��̽��������ͼ�����ʣ�
����д�±�������������ͼ��
| x | ���� | 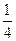 | 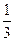 | 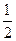 | 1 | 2 | 3 | 4 | ���� |
| y | ���� | | | | | | | | ���� |

|
�䷽�õ�������ͨ���䷽����(x��0)����Сֵ��
�������
����������������������龳���е����⣬ֱ��д���𰸣�
����������12�֣�
�����龳
��֪���ε����Ϊa��aΪ������a��0�������þ��εij�Ϊ����ʱ�������ܳ���С����Сֵ�Ƕ��٣�
��ѧģ��
��þ��εij�Ϊx���ܳ�Ϊy����y��x�ĺ�����ϵʽΪ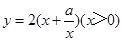 ��
��
̽���о�
�����ǿ��Խ����ǰ�о������ľ��飬��̽������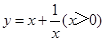 ��ͼ�����ʣ�
��ͼ�����ʣ�
�� ��д�±�������������ͼ��
| x | �� | 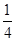 | 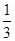 | 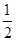 | 1 | 2 | 3 | 4 | �� |
| y | �� | | | | | | | | �� |
��������κ���y=ax2��bx��c��a��0�������С��ֵʱ������ͨ���۲�ͼ������ͨ���䷽�õ�������ͨ���䷽����
 (x��0)����Сֵ��
(x��0)����Сֵ���������
����������������������龳���е����⣬ֱ��д���𰸣�