题目内容
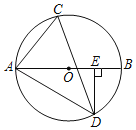
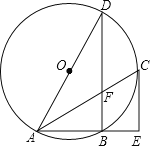
【题目】如图，点A、B、C、D是⊙O上的四个点，AD是⊙O的直径，过点C的切线与AB的延长线垂直于点E，连接AC、BD相交于点F．
（1）求证：AC平分∠BAD；
（2）若⊙O的半径为
，AC＝6，求DF的长．
【答案】（1）证明见解析；（2）
．
【解析】
（1）连接OC，先证明OC∥AE，从而得∠OCA＝∠EAC，再利用OA＝OC得∠OAC＝∠OCA，等量代换即可证得答案；
（2）设OC交BD于点G，连接DC，先证明△ACD∽△AEC，从而利用相似三角形的性质解得
，再利用
＝cos∠FDC，代入相关线段的长可求得DF．
（1）证明：如图，连接OC
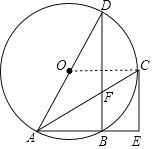
∵过点C的切线与AB的延长线垂直于点E，
∴OC⊥CE，CE⊥AE
∴OC∥AE
∴∠OCA＝∠EAC
∵OA＝OC
∴∠OAC＝∠OCA
∴∠OAC＝∠EAC，即AC平分∠BAD；
（2）如图，设OC交BD于点G，连接DC
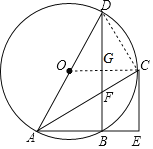
∵AD为直径
∴∠ACD＝90°，∠ABD＝90°
∵CE⊥AE
∴DB∥CE
∵OC⊥CE
∴OC⊥BD
∴DG＝BG
∵∠OAC＝∠EAC，∠ACD＝90°＝∠E
∴△ACD∽△AEC
∴
∵⊙O的半径为
，AC＝6
∴AD＝7，
∴
∴
易得四边形BECG为矩形
∴DG＝BG＝
∵＝cos∠FDC
∴
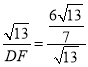
解得：
∴DF的长为.
【题目】为了解学生每天的睡眠情况，某初中学校从全校 800 名学生中随机抽取了 40 名学生，调查了他们平均每天的睡眠时间（单位： h） ，统计结果如下：
9，8，10.5，7，9，8，10，9.5，8，9，9.5，7.5，9.5，9，8.5，7.5，10，9.5，8，9，
7，9.5，8.5，9，7，9，9，7.5，8.5，8.5，9，8，7.5，9.5，10，9.5，8.5，9，8，9.
在对这些数据整理后，绘制了如下的统计图表：
睡眠时间分组统计表 睡眠时间分布情况
组别 | 睡眠时间分组 | 人数（频数） |
1 | 7≤t＜8 | m |
2 | 8≤t＜9 | 11 |
3 | 9≤t＜10 | n |
4 | 10≤t＜11 | 4 |
请根据以上信息，解答下列问题：
（1） m = ， n = ， a = ， b = ；
（2）抽取的这 40 名学生平均每天睡眠时间的中位数落在 组（填组别） ；
（3）如果按照学校要求，学生平均每天的睡眠时间应不少于 9 h，请估计该校学生中睡眠时间符合要求的人数．
