题目内容
【题目】如图，在矩形ABCD中，AB＝6，AD＝8，点M，N分别为AD，AC上的动点（不含端点），AN＝DM，连结点M与矩形的一个顶点，以该线段为直径作⊙O，当点N和矩形的另一个顶点也在⊙O上时，线段DM的长为_____．
【答案】
或
．
【解析】
分两种情形：如图1中，当点N在CM为直径的圆上时，如图2中，当点N在BM为直径的圆上时，分别利用相似三角形的性质构建方程解决问题即可．
∵四边形ABCD是矩形，
∴∠ADC=90°，AB=CD=6，BC=AD=8，
∴AC=
=10，
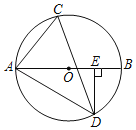
如图1中，当点N在CM为直径的圆上时，设DM=AN=x．
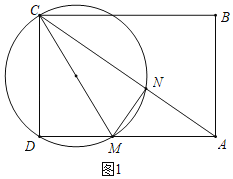
∵CM为直径，
∴∠CNM=90°，
∵∠MAN=∠CAD， ∠ANM=∠ADC=90°，
∴△ANM∽△ADC，
∴
，
∴
，
解得x=
，
∴DM=；
如图2中，当点N在BM为直径的圆上时，设BC与圆的交点为H，连接MH，NH．设DM=AN=y．
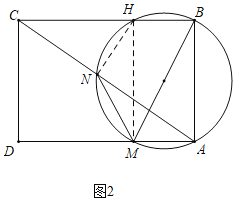
∵BM是直径，
∴∠MHB=90°，
∴∠MHC=∠D=∠DCH=90°，
∴四边形CDMH是矩形，
∴CH=DM=y，
∵∠NCH=∠BCA，∠CHN=∠CAB，
∴△CNH∽△CBA，
∴
，
∴
，
解得y=
，
∴DM=，
故答案为：或．
练习册系列答案
名校课堂系列答案
相关题目
【题目】某市水费采用阶梯收费制度，即：每月用水不超过15吨时，每吨需缴纳水费a元，每月用水量超过15吨时，超过15吨的部分按每吨提高b元缴纳下表是嘉琪家一至四月份用水量和缴纳水费情况．根据表格提供的数据，回答：
月份 | 一 | 二 | 三 | 四 |
月用水量（吨） | 14 | 18 | 16 | 13 |
水费（元） | 42 | 60 | 50 | 39 |
（1）a＝ 元；b＝ 元；
（2）求月缴纳水费p（元）与月用水量t（吨）之间的函数关系式；
（3）若嘉琪家五月和六月的月缴水费相差24元，求这两月用水量差的最小值．
