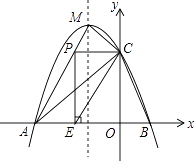��Ŀ����
����Ŀ����ֱ������ϵxOy�У�A��0��2����B����1��0��������ABO������ת��ƽ�Ʊ仯��õ���ͼ1��ʾ�ġ�BCD��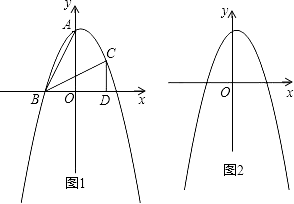
��1����A��B��C����������ߵĽ���ʽ��
��2������AC����P��λ���߶�BC�Ϸ�����������һ���㣬��ֱ��PC����ABC������ֳ�1��3�����֣����ʱ��P�����ꣻ
��3���ֽ���ABO����BCD�ֱ����¡�������1��2���ٶ�ͬʱƽ�ƣ�����ڴ��˶������С�ABO���BCD�ص�������������ֵ��
���𰸡�
��1��
�⣺��A��0��2����B����1��0��������ABO������ת��ƽ�Ʊ仯�õ���BCD��
��BD=OA=2��CD=OB=1����BDC=��AOB=90�㣮
��C��1��1����
�辭��A��B��C����������߽���ʽΪy=ax2+bx+c��
���� 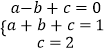 ��
��
�� 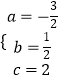
�������߽���ʽΪy=�� ![]() x2+
x2+ ![]() x+2
x+2
��2��
�⣺��ͼ1��ʾ��
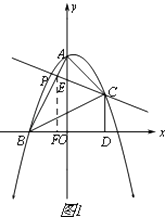
��ֱ��PC��AB���ڵ�E��
��ֱ��PC����ABC������ֳ�1��3�����֣�
�� ![]() =
= ![]() ��
�� ![]() =3��
=3��
��E��EF��OB�ڵ�F����EF��OA��
���BEF�ס�BAO��
�� ![]() ��
��
�൱ ![]() =
= ![]() ʱ��
ʱ�� ![]() ��
��
��EF= ![]() ��BF=
��BF= ![]() ��
��
��E���� ![]() ��
�� ![]() ��
��
��ֱ��PC����ʽΪy=�� ![]() x+
x+ ![]() ��
��
�ੁ ![]() x2+
x2+ ![]() x+2=��
x+2=�� ![]() x+
x+ ![]() ��
��
��x1=�� ![]() ��x2=1����ȥ����
��x2=1����ȥ����
��P���� ![]() ��
�� ![]() ����
����
�� ![]() ʱ��ͬ���ɵã�P����
ʱ��ͬ���ɵã�P���� ![]() ��
�� ![]() ��
��
��3��
�⣺���ABOƽ�Ƶľ���Ϊt����A1B1O1���B2C1D1�ص����ֵ����ΪS��
(i) ��0��t�� ![]() ʱ����A1B1O1���B2C1D1�ص�����Ϊ�ı��Σ�
ʱ����A1B1O1���B2C1D1�ص�����Ϊ�ı��Σ�
��ƽ�Ƶã�A1B1�Ľ���ʽΪy=2x+2��t��A1B1��x�ύ������ΪM�� ![]() ��0����
��0����
C1B2�Ľ���ʽΪy= ![]() x+t+
x+t+ ![]() ��C1B2��y�ύ������ΪN��0��t+
��C1B2��y�ύ������ΪN��0��t+ ![]() ����
����
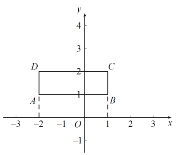
����ͼ2����C1D1��y���Ҳ�ʱ����0��t�� ![]() ʱ���ص����������ı���ONQM��
ʱ���ص����������ı���ONQM��
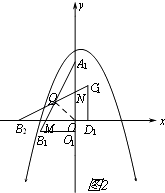
��A1B1��x�ύ�ڵ�M��C1B2��y�ύ�ڵ�N��A1B1��C1B2���ڵ�Q������OQ��
�� 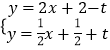 ��
��
�� 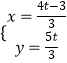 ��
��
��Q�� ![]() ��
�� ![]() ����
����
��S=S��QMO+S��QON
= ![]() ��
�� ![]() ��
�� ![]() +
+ ![]() ����t+
����t+ ![]() ����
���� ![]()
=�� ![]() t2+t+
t2+t+ ![]()
=�� ![]() ��t��
��t�� ![]() ��2+
��2+ ![]() ��
��
��0��t�� ![]() ��
��
�൱t= ![]() ʱ��S�����ֵΪ
ʱ��S�����ֵΪ ![]() ��
��
����ͼ4����C'D'��y����࣬���� ![]() ��t��
��t�� ![]() ʱ����C'�ڡ�A'MO�ڲ������ص��������ı���C'QMD'��
ʱ����C'�ڡ�A'MO�ڲ������ص��������ı���C'QMD'��
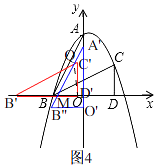
ͬ���ķ����ó���Q�� ![]() ��
�� ![]() ����
����
��S=S��QMD'+S��QON
= ![]() ��[
��[ ![]() ����2t��1��]��
����2t��1��]�� ![]() +
+ ![]() ��1��[
��1��[ ![]() ����2t��1��]
����2t��1��]
=�� ![]() t2+1
t2+1
�� ![]() ��t��
��t�� ![]() ��
��
��S�� ![]() ��
�� ![]()
��ii����ͼ3��ʾ��

�� ![]() ��t��
��t�� ![]() ʱ����A1B1O1���B2C1D1�ص�����Ϊֱ�������Σ�
ʱ����A1B1O1���B2C1D1�ص�����Ϊֱ�������Σ�
��A1B1��x�ύ�ڵ�H��A1B1��C1D1���ڵ�G��
��G��1��2t��4��5t����
��D1H= ![]() +1��2t=
+1��2t= ![]() ��D1G=4��5t��
��D1G=4��5t��
��S= ![]() D1H��D1G=
D1H��D1G= ![]() ��
�� ![]() ����4��5t��=
����4��5t��= ![]() ��5t��4��2��
��5t��4��2��
�൱ ![]() ��t��
��t�� ![]() ʱ��S�����ֵΪ
ʱ��S�����ֵΪ ![]() ��
��
�����������ڴ��˶������С�ABO���BCD�ص�������������ֵΪ ![]() ��
��
����������1������ת��ƽ�Ƶõ�C��1��1�����ô���ϵ������������߽���ʽ����2�����жϳ���BEF�ס�BAO���ٷ�����������м��㣬������Ƚ���������⼴�ɣ���3������ƽ�Ƶõ�A1B1�Ľ���ʽΪy=2x+2��t��A1B1��x�ύ������Ϊ�� ![]() ��0����C1B2�Ľ���ʽΪy=
��0����C1B2�Ľ���ʽΪy= ![]() x+t+
x+t+ ![]() ��C1B2��y�ύ������Ϊ��0��t+
��C1B2��y�ύ������Ϊ��0��t+ ![]() �����ٷ�����������м��㼴�ɣ�
�����ٷ�����������м��㼴�ɣ�