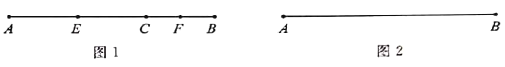题目内容
【题目】已知:OB、OC、OE是∠AOD内的射线,若∠AOD=130°.
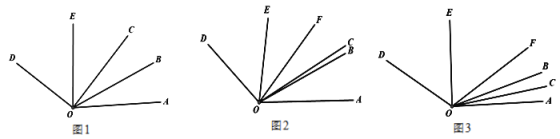
(1)如图1,OB是∠AOC的平分线,OE是∠COD的平分线,∠BOE=_____度;
(2)OF也是∠AOD内的射线,如图2,若∠FOC=20°,OB平分∠AOF,OE平分∠COD,当射线OC绕点O在∠AOF内旋转时,求∠BOE的大小;
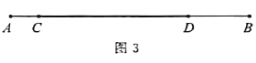
(3)在(2)的条件下,当射线OC从边OA开始绕O点以每秒2°的速度逆时针旋转t秒,如图3,若∠AOB:∠DOE=2:3,求t的值.
【答案】(1)![]() ;(2)∠BOE=55°;(3)t=20.
;(2)∠BOE=55°;(3)t=20.
【解析】
(1)根据角平分线的性质即可得出答案;
(2)方法一:根据角平分线的性质得出∠AOD=2∠BOE+20°即可得出答案;方法二:根据角平分线的性质得出![]() 即可得出答案;
即可得出答案;
(3)设![]() 根据角平分线的性质求出
根据角平分线的性质求出![]() 和
和![]() ,再根据∠AOB:∠DOE=2:3,解出t的值即可得出答案.
,再根据∠AOB:∠DOE=2:3,解出t的值即可得出答案.
解:(1)∵OB是∠AOC的平分线
∴![]()
又OE是∠COD的平分线
∴![]()
∴![]()
(2)方法一:
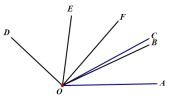
∵ OB平分∠AOF,OE平分∠COD
![]()
![]()
![]()
![]()
![]()
方法二:
∵OB平分∠AOF,OE平分∠COD
∴![]()
∵![]()
∴![]()
![]()
又∵![]()
∴![]()
(3) 由题意可得:![]()
又![]()
∴![]()
又∵OB平分∠AOF
∴![]()
∵![]()
∴![]()
又∵OE平分∠COD
∴![]()
又![]()
解得:![]()

练习册系列答案
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案
相关题目