题目内容
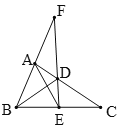
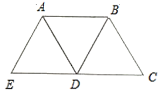
【题目】已知A、F、C、D四点在同一条直线上,AC=DF,AB//DE,EF//BC,
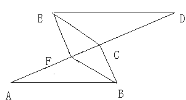
求证:(1)⊿ABC≌⊿DEF
(2)∠CBF=∠FEC
【答案】(1)见详解;(2)见详解
【解析】
(1)首先根据平行线的性质可得∠A=∠D,∠EFD=∠BCA,再加上条件AC=DF可利用ASA证明△ABC≌△DEF;
(2)根据全等三角形性质可得EF=BC,再加上EF∥BC可证明四边形EFBC是平行四边形,根据平行四边形对角相等可得∠CBF=∠FEC.
证明:(1)∵AB∥DE,
∴∠A=∠D,
∵EF∥BC,
∴∠EFD=∠BCA,
在△ABC和△DEF中,
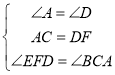 ,
,
∴△ABC≌△DEF(ASA);
(2)∵△ABC≌△DEF,
∴EF=BC
∵EF∥BC,
∴四边形EFBC是平行四边形,
∴∠CBF=∠FEC.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目