题目内容
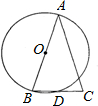 如图,等腰三角形ABC的底边BC的长为a,以腰AB为直径的⊙O交BC于点D.则BD的长为
如图,等腰三角形ABC的底边BC的长为a,以腰AB为直径的⊙O交BC于点D.则BD的长为| a |
| 2 |
| a |
| 2 |
分析:连接AD,由AB为直径,即可推出∠ADB=90°,再根据等腰三角形的底边上的高的性质,即可推出BD=CD,然后根据BC=a,即可推出BD的长度.
解答:解:连接AD,
∵AB为直径,
∴∠ADB=90°,即AD⊥BC,
∵等腰三角形ABC,
∴BD=CD,
∵BC=a,
∴BD=
.
故答案为
.

∵AB为直径,
∴∠ADB=90°,即AD⊥BC,
∵等腰三角形ABC,
∴BD=CD,
∵BC=a,
∴BD=
| a |
| 2 |
故答案为
| a |
| 2 |

点评:本题主要考查圆周角定理,等腰三角形底边上的高的性质,关键在于根据A相关的定理推出AD⊥BC,BD=CD.

练习册系列答案
 核心素养学练评系列答案
核心素养学练评系列答案 单元期中期末卷系列答案
单元期中期末卷系列答案
相关题目
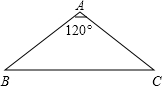 如图,等腰三角形ABC的顶角为120°,底边BC=
如图,等腰三角形ABC的顶角为120°,底边BC=
| ||
| 2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
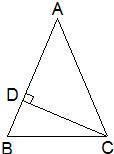 9、如图,等腰三角形ABC中,AB=AC,∠A=44°,CD⊥AB于D,则∠DCB等于( )
9、如图,等腰三角形ABC中,AB=AC,∠A=44°,CD⊥AB于D,则∠DCB等于( ) (1)他们的说法合理吗?为什么?
(1)他们的说法合理吗?为什么?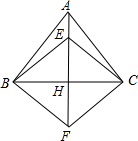 如图,等腰三角形ABC中,AB=AC,AH垂直BC,点E是AH上一点,延长AH至点F,使FH=EH,
如图,等腰三角形ABC中,AB=AC,AH垂直BC,点E是AH上一点,延长AH至点F,使FH=EH,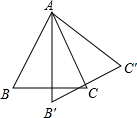 如图,等腰三角形ABC(AB=AC)的底角为50°,绕点A逆时针旋转一定角度后得△AB′C′,那么△AB′C′绕点A旋转
如图,等腰三角形ABC(AB=AC)的底角为50°,绕点A逆时针旋转一定角度后得△AB′C′,那么△AB′C′绕点A旋转