题目内容
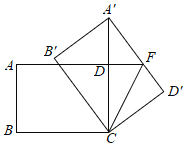
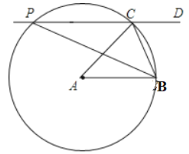
【题目】已知:如图,![]() ABC为锐角三角形,AB=BC,CD∥AB.
ABC为锐角三角形,AB=BC,CD∥AB.
求作:线段BP,使得点P在直线CD上,且∠ABP=![]() .
.
作法:①以点A为圆心,AC长为半径画圆,交直线CD于C,P两点;②连接BP.线段BP就是所求作线段.
(1)使用直尺和圆规,依作法补全图形(保留作图痕迹)
(2)完成下面的证明.
证明:∵CD∥AB,
∴∠ABP= .
∵AB=AC,
∴点B在⊙A上.
又∵∠BPC=![]() ∠BAC( )(填推理依据)
∠BAC( )(填推理依据)
∴∠ABP=![]() ∠BAC
∠BAC
【答案】(1)见解析;(2)∠BPC,在同圆或等圆中同弧所对的圆周角等于它所对圆心角的一半
【解析】
(1)按照作法的提示,逐步作图即可;
(2)利用平行线的性质证明:![]() 再利用圆的性质得到:∠BPC=
再利用圆的性质得到:∠BPC=![]() ∠BAC,从而可得答案.
∠BAC,从而可得答案.
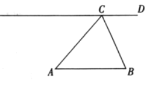
解:(1)依据作图提示作图如下:
(2)证明:∵CD∥AB,
∴∠ABP= ![]() .
.
∵AB=AC,
∴点B在⊙A上.
又∵∠BPC=![]() ∠BAC(在同圆或等圆中同弧所对的圆周角等于它所对圆心角的一半. )(填推理依据)
∠BAC(在同圆或等圆中同弧所对的圆周角等于它所对圆心角的一半. )(填推理依据)
∴∠ABP=![]() ∠BAC
∠BAC
故答案为:∠BPC;在同圆或等圆中同弧所对的圆周角等于它所对圆心角的一半.

【题目】小云统计了自己所住小区5月1日至30日的厨余垃圾分出量(单位:千克),相关信息如下:
![]() .小云所住小区5月1日至30日的厨余垃圾分出量统计图:
.小云所住小区5月1日至30日的厨余垃圾分出量统计图:
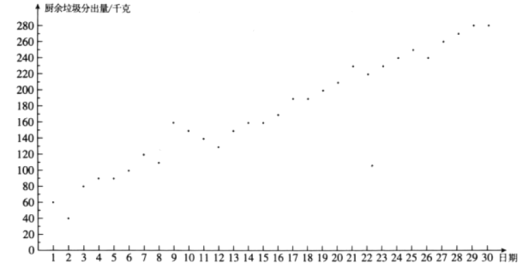
![]() .小云所住小区5月1日至30日分时段的厨余垃圾分出量的平均数如下:
.小云所住小区5月1日至30日分时段的厨余垃圾分出量的平均数如下:
时段 | 1日至10日 | 11日至20日 | 21日至30日 |
平均数 | 100 | 170 | 250 |
(1)该小区5月1日至30日的厨余垃圾分出量的平均数约为 (结果取整数)
(2)已知该小区4月的厨余垃圾分出量的平均数为60,则该小区5月1日至30日的厨余垃圾分出量的平均数约为4月的 倍(结果保留小数点后一位);
(3)记该小区5月1日至10日的厨余垃圾分出量的方差为![]() 5月11日至20日的厨余垃圾分出量的方差为
5月11日至20日的厨余垃圾分出量的方差为![]() ,5月21日至30日的厨余垃圾分出量的方差为
,5月21日至30日的厨余垃圾分出量的方差为![]() .直接写出
.直接写出![]() 的大小关系.
的大小关系.