题目内容
【题目】在如图所示的方格中，每个小方格都是边长为1个单位长度的正方形，
的三个顶点都在格点（小方格的顶点）上．
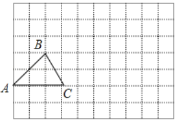
（1）请建立适当的平面直角坐标系，使
，
，并写出点
的坐标；
（2）在（1）的条件下，将先向右平移4个单位长度再向上平移2个单位长度后可得到
，请在图中画出平移后的，并分别写出点
，
，
的坐标．
【答案】（1）(0，1)，坐标系见详解；（2）
(2，1)，
(4，3)，
(5，1)，图形见详解
【解析】
（1）由
，
，可确定原点的位置，进而建立平面直角坐标系，然后写出点B的坐标，即可；
（2）先找到
各个顶点的对应点的位置，再顺次连接起来，即可．
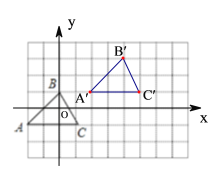
（1）根据题意，建立适当的平面直角坐标系，如图所示：
∴点B的坐标为：(0，1)；
（2）
如图所示，(2，1)，(4，3)，(5，1)．
考前必练系列答案
【题目】国务院办公厅2015年3月16日发布了《中国足球改革的总体方案》，这是中国足球历史上的重大改革．为了进一步普及足球知识，传播足球文化，我市举行了“足球进校园”知识竞赛活动，为了解足球知识的普及情况，随机抽取了部分获奖情况进行整理，得到下列不完整的统计图表：
获奖等次 | 频数 | 频率 |
一等奖 | 10 | 0.05 |
二等奖 | 20 | 0.10 |
三等奖 | 30 | b |
优胜奖 | a | 0.30 |
鼓励奖 | 80 | 0.40 |
请根据所给信息，解答下列问题：
（1）a= ， b= ， 且补全频数分布直方图；
（2）若用扇形统计图来描述获奖分布情况，问获得优胜奖对应的扇形圆心角的度数是多少？
（3）在这次竞赛中，甲、乙、丙、丁四位同学都获得一等奖，若从这四位同学中随机选取两位同学代表我市参加上一级竞赛，请用树状图或列表的方法，计算恰好选中甲、乙二人的概率．
【题目】在如图中，每个正方形由边长为1的小正方形组成：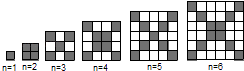
（1）观察图形，请填写下列表格：
正方形边长 | 1 | 3 | 5 | 7 | … | n（奇数） |
黑色小正方形个数 |
正方形边长 | 2 | 4 | 6 | 8 | … | n（偶数） |
黑色小正方形个数 |
（2）在边长为n（n≥1）的正方形中，设黑色小正方形的个数为P1 ， 白色小正方形的个数为P2 ， 问是否存在偶数n，使P2=5P1？若存在，请写出n的值；若不存在，请说明理由．
