题目内容
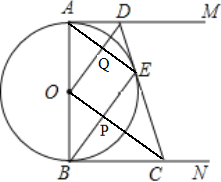
【题目】如图所示,AB是⊙O的直径,AM、BN是⊙O的两条切线,D、C分别在AM、BN上,DC切⊙O于点E,连接OD、OC、BE、AE,BE与OC相交于点P,AE与OD相交于点Q,已知AD=4,BC=9.以下结论:
①⊙O的半径为![]() ②OD∥BE ③PB=
②OD∥BE ③PB=![]()
![]() ④tan∠CEP=
④tan∠CEP=![]()
其中正确的结论有( )
A.1个 B.2个 C.3个 D.4个
【答案】B.
【解析】
试题分析:①连接OE,则OE⊥DC,易证明四边形ABCD是梯形,则其中位线长等于![]() (4+9)=
(4+9)=![]() ,而梯形ABCD的中位线平行于两底,显而易见,中位线的长(斜边)大于直角边(或运用垂线段最短判定),故可判断①错误;②先证明△AOD≌△EOD,得出∠AOD=∠EOD=
,而梯形ABCD的中位线平行于两底,显而易见,中位线的长(斜边)大于直角边(或运用垂线段最短判定),故可判断①错误;②先证明△AOD≌△EOD,得出∠AOD=∠EOD=![]() ∠AOE,再运用同弧所对的圆周角等于圆心角的一半证明∠AOD=∠ABE,从而得出OD∥BE,故②正确;③由①知OB=6,根据勾股定理,OC=
∠AOE,再运用同弧所对的圆周角等于圆心角的一半证明∠AOD=∠ABE,从而得出OD∥BE,故②正确;③由①知OB=6,根据勾股定理,OC=![]() =
=![]() =3
=3![]() ;易证△OPB∽△OBC,则
;易证△OPB∽△OBC,则![]() ,所PB=
,所PB=![]() =
=![]() =
=![]()
![]() ,③正确;④易知∠CEP>∠ECP,所以CP>PE,故tan∠CEP=
,③正确;④易知∠CEP>∠ECP,所以CP>PE,故tan∠CEP=![]() 错误.故答案选B.
错误.故答案选B.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目