题目内容
【题目】(1)观察推理:如图1,△ABC中,∠ACB=90°,AC=BC,直线l过点C,点A,B在直线l同侧,BD⊥l,AE⊥l,垂足分别为D,E.求证:△AEC≌△CDB;
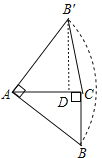
(2)类比探究:如图2,Rt△ABC中,∠ACB=90°,AC=2,将斜边AB绕点A逆时针旋转90°至AB',连接B′C,求△AB′C的面积.
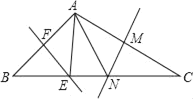
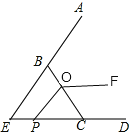
(3)拓展提升:如图3,等边△EBC中,EC=BC=3cm,点O在BC上且OC=2cm,动点P从点E沿射线EC以lcm/s速度运动,连接OP,将线段OP绕点O逆时针旋转120°得到线段OF,设点P运动的时间为t秒.
①当t=______秒时,OF∥ED.
②当t=______秒时,点F恰好落在射线EB上.

【答案】(1)见解析;(2)2;(3)①1;②4
【解析】
(1)先利用等角的余角相等得到∠EAC=∠BCD,根据“AAS”证明△AEC≌△CDB即可;(2)如图,作B′D⊥AC于D,利用等角的余角相等得到∠B=∠B′AC,利用AAS可证明△B′AD≌△ABC,得到B′D=AC=2,然后根据三角形面积公式计算即可得答案;(3)①如图,由题意得EP=t,则PC=3﹣t,由平行线的性质可得∠FOC=BCE=60°,根可旋转的性质可得∠PQC=60°,可证明△COP是等边三角形,可得PC=OC=2,即可求t的值;②如图,利用旋转的性质得∠FOP=120°,OP=OF,利用外角性质及角的和差关系可得∠1=∠3,利用AAS可证明△BOF≌△CPO,可得PC=OB=1,则EP=EC+PC=4,然后计算点P运动的时间t即可.
(1)∵BD⊥l,AE⊥l,
∴∠AEC=∠BDC=90°,
∵∠EAC+∠ACE=90°,∠BCD+∠ACE=90°,
∴∠EAC=∠BCD,
在△AEC和△CDB中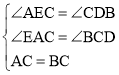 ,
,
∴△AEC≌△CDB(AAS).
(2)如图,作B′D⊥AC于D,
∴∠ADB′=90°,
∵斜边AB绕点A逆时针旋转90°至AB′,
∴AB′=AB,∠B′AB=90°,即∠B′AC+∠BAC=90°,
∵∠B+∠CAB=90°,
∴∠B=∠B′AC,
在△B′AD和△ABC中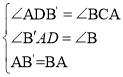 ,
,
∴△B′AD≌△ABC(AAS),
∴B′D=AC=2,
∴△AB′C的面积=![]() AC·B′D=
AC·B′D=![]() ×2×2=2.
×2×2=2.
(3)①如图,由题意得:EP=t,则PC=3﹣t,
∵OF∥ED
∴∠FOC=BCE,
∵线段OP绕点O逆时针旋转120°得到线段OF,
∴∠POF=120°,
∴∠POC=60°,
∵△BEC是等边三角形,
∴∠BCE=60°
∴△COP是等边三角形,
∴PC=OC=2,
∴2=3﹣t,
∴t=1,
即当t=1秒时,OF∥ED,
故答案为:1
②如图,∵OC=2,
∴OB=BC﹣OC=1,
∵线段OP绕点O逆时针旋转120°得到线段OF,
∴∠FOP=120°,OP=OF,
∴∠1+∠2=60°,
∵△BCE为等边三角形,
∴∠BCE=∠CBE=60°,
∴∠FBO=120°,∠PCO=120°,
∴∠2+∠3=∠BCE=60°,
∴∠1=∠3,
在△BOF和△CPO,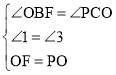 ,
,
∴△BOF≌△CPO(AAS),
∴PC=OB=1,
∴EP=EC+PC=3+1=4,
∴点P运动的时间t=![]() =4s,
=4s,

故答案为:4

 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案