题目内容
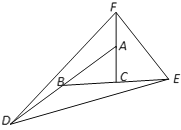
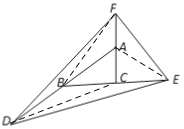
【题目】如图,将△ABC的三边AB,BC,CA分别拉长到原来的两倍,得点D,E,F,已知△DEF的面积为42,则△ABC的面积为( )
A.14B.7C.6D.3
【答案】C
【解析】
连接BF、CD、AE,根据三角形中线的性质可得S△ABC=S△ACE=S△ABF=S△BCD,S△BCD=S△ECD,S△BDF=S△ABF,S△AEF=S△ACE,即可得出S△DEF=7S△ABC,即可求出△ABC的面积.
如图,连接BF、CD、AE,
∵△ABC的三边AB,BC,CA分别拉长到原来的两倍,
∴点A、B、C是CF、AD、BE的中点,
∴S△ABC=S△ACE=S△ABF=S△BCD,S△BCD=S△ECD,S△BDF=S△ABF,S△AEF=S△ACE,
∴S△DEF=7S△ABC,
∵S△DEF=42,
∴S△ABC=6,
故选:C.

练习册系列答案
相关题目