Question

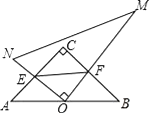
【题目】在四边形ABCD中如图，∠A＝∠B＝90°，将△AED、△DCF分别沿着DE、DF翻折，点A、C都分别与EF上的点G重合．

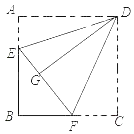
（1）求证：四边形ABCD是正方形；（2）若AB＝6，点F是BC的中点，求AE的长．

Answer 1

【答案】（1）见解析；（2）AE＝2．

【解析】

（1）首先证明四边形ABCD是矩形，再证明DA=DC即可解决问题；
（2）设AE=EG=x，利用Rt△BEF，根据勾股定理构建方程即可解决问题；

解：（1）证明：由翻折的性质可知：△ADE≌△GDE，△DCF≌△DGF，

∴AD＝DG＝DC，∠A＝∠DGE＝90°，∠C＝∠DGF＝90°，

∵∠B＝90°，

∴四边形ABCD是矩形，

∵DA＝DC，

∴四边形ABCD是正方形．

（2）设AE＝EG＝x，则BE＝6﹣x，EF＝x+3，BF＝3，

在Rt△BEF中，∵EF2＝BE2+BF2，

∴（x+3）2＝（6﹣x）2+32，

∴x＝2，

∴AE＝2．