题目内容
【题目】如图,已知AB为⊙O的直径,AC为弦,OD∥BC,交AC于D,BC=4cm.
(1)求证:AC⊥OD;
(2)求OD的长;
(3)若sinA=![]() ,求⊙O的直径.
,求⊙O的直径.
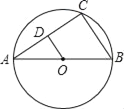
【答案】(1)证明见解析;(2)OD= 2cm;(3)⊙O的直径是8cm.
【解析】试题分析:(1)根据直径所对的圆周角是直角可得∠C=90°,再根据两直线平行,同位角相等可得∠ADO=∠C=90°,然后根据垂直的定义证明即可;
(2)先判断出OD是△ABC的中位线,再根据三角形的中位线平行于第三边并且等于第三边的一半可得OD=![]() BC;
BC;
(3)先根据∠A的正弦求出∠A=30°,再根据直角三角形30°角所对的直角边等于斜边的一半可得BC=![]() AB,然后求解即可.
AB,然后求解即可.
试题解析:(1)证明:∵AB是⊙O的直径,
∴∠C=90°,
∵OD∥BC,
∴∠ADO=∠C=90°,
∴AC⊥OD;
(2)解:∵OD∥BC,O是AB的中点,
∴OD是△ABC的中位线,
∴OD=![]() BC=
BC=![]() ×4=2cm;
×4=2cm;
(3)解:∵2sinA﹣1=0,
∴sinA=![]() ,
,
∴∠A=30°,
在Rt△ABC,∵∠A=30°,
∴BC=![]() AB,
AB,
∴AB=2BC=8cm,
即⊙O的直径是8cm.

练习册系列答案
相关题目