题目内容
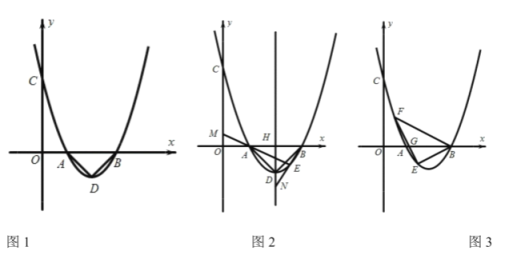
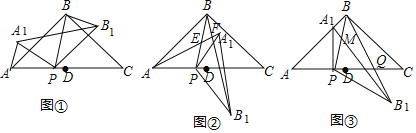
【题目】在△ABC中，AB＝BC，∠ABC＝90°，D为AC中点，点P是线段AD上的一点，点P与点A、点D不重合），连接BP．将△ABP绕点P按顺时针方向旋转α角（0°＜α＜180°），得到△A1B1P，连接A1B1、BB1
（1）如图①，当0°＜α＜90°，在α角变化过程中，请证明∠PAA1＝∠PBB1．
（2）如图②，直线AA1与直线PB、直线BB1分别交于点E，F．设∠ABP＝β，当90°＜α＜180°时，在α角变化过程中，是否存在△BEF与△AEP全等？若存在，求出α与β之间的数量关系；若不存在，请说明理由；
（3）如图③，当α＝90°时，点E、F与点B重合．直线A1B与直线PB相交于点M，直线BB′与AC相交于点Q．若AB＝
，设AP＝x，CQ＝y，求y关于x的函数关系式．
【答案】（1）证明见解析；（2）α﹣2β＝90°；（3）y＝
．
【解析】
（1）先利用旋转得出两个顶角相等的两个等腰三角形，即可得出结论；
（2）假设存在，然后利用确定的出AE=BE，即可求出∠A1AP=∠AA1P，最后用∠BAC=45°建立方程化简即可；
（3）先判断出△ABQ∽△CPB，得出比例式即可得出结论．
解：（1）∵将△ABP绕点P按顺时针方向旋转α角（0°＜α＜180°），得到△A1B1P，
∴∠APA1＝∠BPB1＝α，AP＝A1P，BP＝B1P，
∴∠AA1P＝∠A1AP＝
＝
，∠BB1P＝∠B1BP＝
＝，
∴∠PAA1＝∠PBB1，
（2）假设在α角变化的过程中，存在△BEF与△AEP全等，
∵△BEF与△AEP全等，
∴AE＝BE，
∴∠ABE＝∠BAE＝β，
∵AP＝A1P，
∴∠A1AP＝∠AA1P＝，
∵AB＝BC，∠ABC＝90°，
∴∠BAC＝45°，
∴β+＝45°，
∴α﹣2β＝90°，
（3）当α＝90°时，
∵AP＝A1P，BP＝B1P，∠APA1＝∠BPB2＝90°，
∴∠A＝∠PBB1＝45°，
∵∠A＝∠C，∠AQB＝∠C+∠QBC＝45°+∠QBC＝∠PBC，
∴△ABQ∽△CPB，
∴
，
∵AB＝
，
∴
，
∴y＝．
