Question

【题目】已知抛物线与轴交于两点(点在点的左边)，与轴交于点，顶点为.

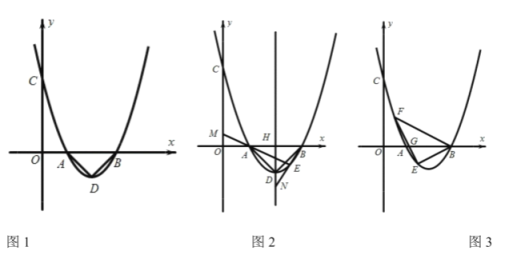
（1）如图1，请求出三点的坐标;

（2）点为轴下方抛物线上一动点.

①如图2，若时，抛物线的对称轴交轴于点,直线交轴于点，直线交对称轴于点，求的值;

②如图3，若时，点在轴上方的抛物线上运动，连接交轴于点，且满足当线段运动时，的度数大小发生变化吗?若不变,请求出的值若变化，请说明理由.

Answer 1

【答案】（1）；（2）①2； ②=4，理由见解析

【解析】

（1）令y=0，代入函数解析式，令x=0，代入函数解析式，即可求解；

（2）①过点作轴于点，设点，由，，得，从而得，进而即可得到结论；②设点，由题意得：，过点作轴于点,作轴于点,过点作,交的延长线于点，由，得，从而得，结合正切三角函数的定义，即可得到结论．

（1）令y=0代入，得，

解得：，

令x=0代入，得：y=3k，

∴；

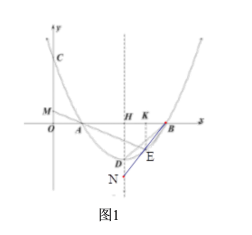
（2）①过点作轴于点，如图1，则，，

∵当时，，对称轴为：直线x=2，

∴设点，

，

，

，

；

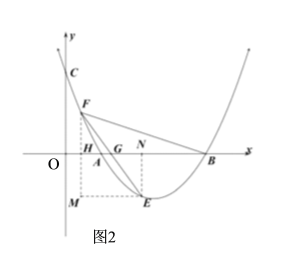
②不会变化，理由如下：

∵当时，，

∴设点，

∵当时，不能满足，

，

如图2，过点作轴于点,作轴于点,过点作,交的延长线于点．

∵，∠FHB=∠ENB=90°，

，

，

，

∵EM∥x轴，

∴∠FGO=∠FEM，

∴点和点在抛物线上运动时，的值不会变化．