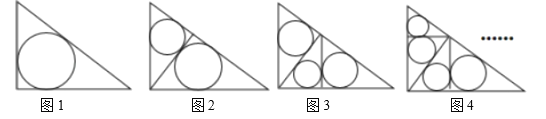
题目内容
【题目】如图![]() ,在直角边分别为
,在直角边分别为![]() 和
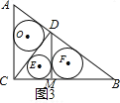
和![]() 的直角三角形中,每多作一条斜边上的高就增加一个三角形的内切圆,依此类推,图10中有
的直角三角形中,每多作一条斜边上的高就增加一个三角形的内切圆,依此类推,图10中有![]() 个直角三角形的内切圆,它们的面积分别记为
个直角三角形的内切圆,它们的面积分别记为![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,则
,则![]() ________.
________.
【答案】π
【解析】
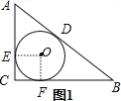
图1,作辅助线构建正方形![]() ,设圆
,设圆![]() 的半径为
的半径为![]() ,根据切线长定理表示出
,根据切线长定理表示出![]() 和
和![]() 的长,利用
的长,利用![]() 列方程求出半径
列方程求出半径![]() 、
、![]() 是直角边,
是直角边,![]() 为斜边),运用圆面积公式
为斜边),运用圆面积公式![]() 求出面积
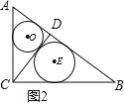
求出面积![]() ;图2,先求斜边上的高
;图2,先求斜边上的高![]() 的长,再由勾股定理求出
的长,再由勾股定理求出![]() 和
和![]() ,利用半径
,利用半径![]() 、
、![]() 是直角边,
是直角边,![]() 为斜边)求两个圆的半径,从而求出两圆的面积和
为斜边)求两个圆的半径,从而求出两圆的面积和![]() ;图3,继续求高
;图3,继续求高![]() 和
和![]() 、
、![]() ,利用半径
,利用半径![]() 、
、![]() 是直角边,
是直角边,![]() 为斜边)求三个圆的半径,从而求出三个圆的面积和
为斜边)求三个圆的半径,从而求出三个圆的面积和![]() ;据此规律进行求解即可.
;据此规律进行求解即可.
图1,过点![]() 做
做![]() ,
,![]() ,垂足为
,垂足为![]() 、
、![]() ,则
,则![]()
![]()
![]() 四边形
四边形![]() 为矩形
为矩形
![]()
![]() 矩形
矩形![]() 为正方形
为正方形
设圆![]() 的半径为
的半径为![]() ,则
,则![]() ,
,![]() ,
,![]()
![]() ,
,![]()
![]()
图2,由![]()
![]()
由勾股定理得:![]() ,
,![]()
由(1)得:![]() 的半径
的半径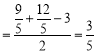 ,
,![]() 的半径
的半径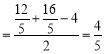
![]()
图3,由![]()
![]()
由勾股定理得:![]() ,
,![]()
由(1)得:![]() 的半径
的半径![]() ,
,![]() 的半径
的半径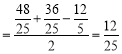 ,
,![]() 的半径
的半径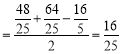
![]()
![]() 图4中的
图4中的![]()
则![]()
故答案为:![]() .
.

练习册系列答案
 全优点练单元计划系列答案
全优点练单元计划系列答案
相关题目