题目内容
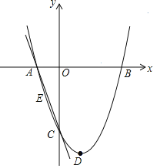
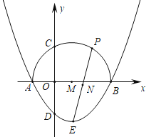
【题目】如图,抛物线![]() 的图象与坐标轴交于点A,B,D,顶点为E,以AB为直径画半圆交y正半轴交于点C,圆心为M,P是半圆上的一动点,连接EP.①点E在⊙M的内部;②CD的长为
的图象与坐标轴交于点A,B,D,顶点为E,以AB为直径画半圆交y正半轴交于点C,圆心为M,P是半圆上的一动点,连接EP.①点E在⊙M的内部;②CD的长为![]() ;③若P与C重合,则∠DPE=15°;④在P的运动过程中,若AP=
;③若P与C重合,则∠DPE=15°;④在P的运动过程中,若AP=![]() ,则PE=
,则PE=![]() ⑤N是PE的中点,当P沿半圆从点A运动至点B时,点N运动的路径长是2π.其中结论正确的是______________
⑤N是PE的中点,当P沿半圆从点A运动至点B时,点N运动的路径长是2π.其中结论正确的是______________
【答案】②③④
【解析】
①ME=2=AM,∴E应该在⊙M上,即可求解;
②CD=2×![]() =3,故CD的长为
=3,故CD的长为![]()
③过点D作DH⊥ME,由DH=1,MD=R=2,故∠DME=30°,则∠DPE=15°,即可求解;
④ AK=AEsinα=2![]() ×
×![]() =
=![]() ,同理EK=
,同理EK=![]() ,则PK=
,则PK=![]() ,即可求解;
,即可求解;
⑤点N的运动轨迹为以R为圆心的半圆,则N运动的路径长=![]() ×2πr=π,
×2πr=π,
解:抛物线![]() 的图象与坐标轴交于点A,B,D,
的图象与坐标轴交于点A,B,D,
则点A、B、D的坐标分别为:(-1,0)、(3,0)、(0,-![]() ),则点M(1,0),
),则点M(1,0),
顶点E的坐标为:(1,-2),AB=4,CO=![]() ,OD=
,OD=![]() ,故点D不在⊙M上;
,故点D不在⊙M上;
①ME=2=AM,∴E应该在⊙M上,故不符合题;
②C是圆M与y轴交点,圆M半径为2,M(1,0)由勾股定理得OC=![]() ,
,
CD=2×![]() =3,故CD的长为
=3,故CD的长为![]() ,符合题意;
,符合题意;
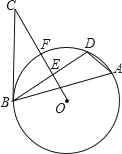
③如图1,连接DP、ME,点D、E均在⊙M上,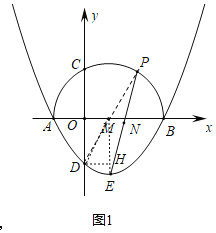
过点D作DH⊥ME于H,
∵DH=1,MD=R=2,
故∠DME=30°,则∠DPE=15°,符合题意;
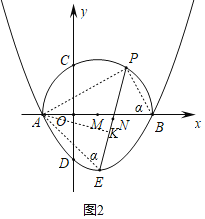
④如图2,连接PB、PA、AE,
∵点B、E均在圆上,则∠ABP=∠AEP=α,
sin∠AEP=sin∠ABP=![]() =sinα,则cosα=
=sinα,则cosα=![]() ,
,
过点A作AK垂直于PE于K,则AK=AEsinα=2![]() ×
×![]() =
=![]() ,EK=AEcosα═
,EK=AEcosα═![]() ,则PK=AK=
,则PK=AK=![]() ,故则PE=
,故则PE=![]() ,符合题意;
,符合题意;
⑤如图3,图中实点G、N、M、F是点N运动中所处的位置,
则GF是等腰直角三角形的中位线,GF=![]() AB=2,ME交AB于点R,则四边形GEFM为正方形,当点P在半圆任意位置时,中点为N,连接MN,则MN⊥PE,连接NR,
AB=2,ME交AB于点R,则四边形GEFM为正方形,当点P在半圆任意位置时,中点为N,连接MN,则MN⊥PE,连接NR,
则NR=![]() ME=MR=RE=RG=RF=
ME=MR=RE=RG=RF=![]() GF=1,则点N的运动轨迹为以R为圆心的半圆,则N运动的路径长=
GF=1,则点N的运动轨迹为以R为圆心的半圆,则N运动的路径长=![]() ×2πr=π,故不符合题意;
×2πr=π,故不符合题意;
故答案为:②③④.

【题目】近年来,“在初中数学教学候总使用计算器是否直接影响学生计算能力的发展”这一问题受到了广泛关注,为此,某校随机调查了n名学生对此问题的看法(看法分为三种:没有影响,影响不大,影响很大),并将调查结果 绘制成如下不完整的统计表和扇形统计图,根据统计图表提供的信息,解答下列问题:
n名学生对使用计算器影响计算能力的发展看法人数统计表
看法 | 没有影响 | 影响不大 | 影响很大 |
学生人数(人) | 40 | 60 | m |

(1)求n的值;
(2)统计表中的m= ;
(3)估计该校1800名学生中认为“影响很大”的学生人数.