题目内容
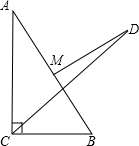
如图,O是△ABC的外心,弦AB的垂直平分线与AB和AC分别相交于点M、N,与BC边的延长线相交于点P,求证:OA2=ON•OP.
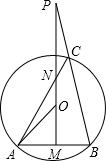

证明:连接OB;
∵PM垂直平分AB,
∴OA=OB,AM=BM,OM⊥AB;
∴∠AOM=∠BOM=
∠AOB;
∵∠ACB=
∠AOB,∴∠ACB=∠AOM;
∴∠NAO+∠ANO=∠P+∠PNC;
∵∠PNC=∠ANO,∴∠P=∠NAO;
∵∠AOM=∠MOB,
∴∠AON=∠BOP;
∴△ANO∽△PBO,
∴
=
,即OA•OB=OP•ON;
∵OA=OB,
∴OA2=ON•OP.
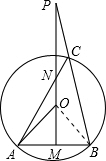
∵PM垂直平分AB,
∴OA=OB,AM=BM,OM⊥AB;
∴∠AOM=∠BOM=
| 1 |
| 2 |
∵∠ACB=
| 1 |
| 2 |
∴∠NAO+∠ANO=∠P+∠PNC;
∵∠PNC=∠ANO,∴∠P=∠NAO;
∵∠AOM=∠MOB,
∴∠AON=∠BOP;
∴△ANO∽△PBO,
∴
| ON |
| OB |
| OA |
| OP |
∵OA=OB,
∴OA2=ON•OP.


练习册系列答案
相关题目