题目内容
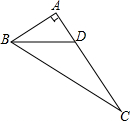
如图，在△ABC中，∠C=90°，M为AB的中点，DM⊥AB，CD平分∠ACB，求证：MD=AM．
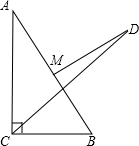
证明：如图，连接CM，设AB、CD相交于点E，
则CM是斜边上的中线，MC=MB=AM，
∴∠MCB=∠B，
∵CD平分∠ACB，∠C=90°，
∴∠BCD=
×90°=45°，
∴∠MCD=∠MCB-45°=∠B-45°，
又∵∠DEM=∠BEC=180°-∠B-45°=135°-∠B，
∴∠D=90°-∠DEM=∠B-45°，
∴∠D=∠MCD，
∴MD=MC，
∴MD=AM．
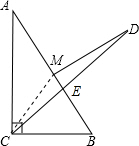
则CM是斜边上的中线，MC=MB=AM，
∴∠MCB=∠B，
∵CD平分∠ACB，∠C=90°，
∴∠BCD=
| 1 |
| 2 |
∴∠MCD=∠MCB-45°=∠B-45°，
又∵∠DEM=∠BEC=180°-∠B-45°=135°-∠B，
∴∠D=90°-∠DEM=∠B-45°，
∴∠D=∠MCD，
∴MD=MC，
∴MD=AM．
练习册系列答案
作业辅导系列答案
同步学典一课多练系列答案
相关题目
