题目内容
已知a1，a2，…a2002均为正数，且满足M=（a1+a2+…+a2001）（a2+a3+…+a2001-a2002），N=（a1+a2+…+a2001-a2002） （a2+a3+…+a2001），则M与N之间的关系是
- A.M＞N
- B.M＜N
- C.M=N
- D.无法确定
B
分析：先设x=a1+a2+…+a2001，y=a2+a3+…+a2001，那么M、N都变成了单项式乘以多项式，计算后比较即可．
解答：设x=a1+a2+…+a2001，y=a2+a3+…+a2001，那么有
M=x（y-a2002）=xy-a2002x，
N=（x-a2002）y=xy-a2002y，
又知a1，a2，a3，…，a2001，a2002均为正数，
∴a2002x＞a2002y，
∴M＜N．
故选B．
点评：本题考查的是单项式乘以多项式，关键是换元法设未知数，变繁为简．
分析：先设x=a1+a2+…+a2001，y=a2+a3+…+a2001，那么M、N都变成了单项式乘以多项式，计算后比较即可．
解答：设x=a1+a2+…+a2001，y=a2+a3+…+a2001，那么有
M=x（y-a2002）=xy-a2002x，
N=（x-a2002）y=xy-a2002y，
又知a1，a2，a3，…，a2001，a2002均为正数，
∴a2002x＞a2002y，
∴M＜N．
故选B．
点评：本题考查的是单项式乘以多项式，关键是换元法设未知数，变繁为简．
练习册系列答案
相关题目
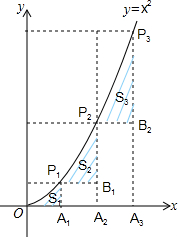如图，已知A1，A2，A3，…，A2012是x轴上的点，且0A1=A1A2=A2A3=…=A2010A2011=A2011A2012=1，分别过点A1，A2，A3，…，A2012作x轴的垂线交二次函数y=x2（x≥0）的图象于点P1，P2，P3，…，P2012，若△OA1P1的面积为S1，过点P1作P1B1⊥A2P2于点B1，记△P1B1P2的面积为S2，过点P2作P2B2⊥A3P3于点B2，记△P2B2P3的面积为S3，…依次进行下去，最后记△P2011B2011P2012的面积为S20121，则