题目内容
【题目】如图,在半径为 ![]() 的
的 ![]() 中,弦
中,弦 ![]() ,
,![]() 是弦
是弦 ![]() 所对的优弧上的动点,连接
所对的优弧上的动点,连接 ![]() , 过点
, 过点 ![]() 作
作 ![]() 的垂线交射线
的垂线交射线 ![]() 于点
于点 ![]() ,当
,当 ![]() 是等腰三角形时,线段
是等腰三角形时,线段 ![]() 的长为____.
的长为____.

【答案】![]() 或8或
或8或![]()
【解析】试题分析:①当BA=BP时,
易得AB=BP=BC=8,即线段BC的长为8.
②当AB=AP时,如图1,延长AO交PB于点D,过点O作OE⊥AB于点E,则AD⊥PB,AE=![]() AB=4,
AB=4,
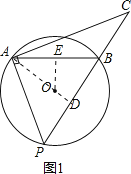
∴BD=DP,
在Rt△AEO中,AE=4,AO=5,
∴OE=3,
易得△AOE∽△ABD,
∴![]() ,
,
∴BD=![]() ,
,
∴BD=PD=![]() ,即PB=
,即PB=![]() ,
,
∵AB=AP=8,
∴∠ABD=∠P,
∵∠PAC=∠ADB=90°,
∴△ABD∽△CPA,
∴![]() ,
,
∴CP=![]() ,
,
∴BC=CP-BP=![]()
![]() =
=![]() ;
;
③当PA=PB时
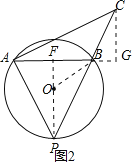
如图2,连接PO并延长,交AB于点F,过点C作CG⊥AB,交AB的延长线于点G,连接OB,
则PF⊥AB,
∴AF=FB=4,
在Rt△OFB中,OB=5,FB=4,
∴OF=3,
∴FP=8,
易得△PFB∽△CGB,
∴![]() ,
,
设BG=t,则CG=2t,
易得∠PAF=∠ACG,
∵∠AFP=∠AGC=90°,
∴△APF∽△CAG,
∴![]() ,
,
∴![]() ,
,
解得t![]() ,
,
在Rt△BCG中,BC=![]() t=
t=![]() ,
,
综上所述,当△PAB是等腰三角形时,线段BC的长为8,![]() ,
,![]() ,
,
故答案为:8,![]() ,
,![]() .
.

练习册系列答案
相关题目