ĖâÄŋÄÚČÝ
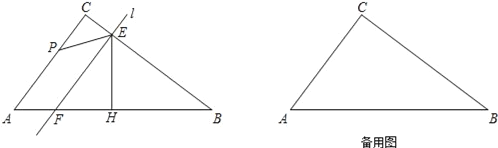
ĄūĖâÄŋĄŋČįÍžĢŽÔÚRtĄũABCÖÐĢŽĄÏC=90ĄãĢŽAC=9ĢŽAB=15ĢŽķŊĩãPīÓĩãAģö·ĒĢŽŅØACĄúCBĄúBAąßÔËķŊĢŽĩãPÔÚACĄĒCBĄĒBAąßÉÏÔËķŊĩÄËŲķČ·ÖąðΊÃŋÃë3ĄĒ4ĄĒ5ļöĩĨÎŧĢŽÖąÏßlīÓÓëACÖØšÏĩÄÎŧÖÃŋŠĘžĢŽŌÔÃŋÃë![]() ļöĩĨÎŧĩÄËŲķČŅØCB·―ÏōŌÆķŊĢŽŌÆķŊđýģĖÖÐąĢģÖlĄÎACĢŽĮŌ·ÖąðÓëCBĢŽABąß―ŧÓÚEĢŽFÁ―ĩãĢŽĩãPÓëÖąÏßlÍŽĘąģö·ĒĢŽÉčÔËķŊĩÄĘąžäΊtÃëĢŽĩąĩãPĩÚŌŧīÎŧØĩ―ĩãAĘąĢŽĩãPšÍÖąÏßlÍŽĘąÍĢÖđÔËķŊĢŪ
ļöĩĨÎŧĩÄËŲķČŅØCB·―ÏōŌÆķŊĢŽŌÆķŊđýģĖÖÐąĢģÖlĄÎACĢŽĮŌ·ÖąðÓëCBĢŽABąß―ŧÓÚEĢŽFÁ―ĩãĢŽĩãPÓëÖąÏßlÍŽĘąģö·ĒĢŽÉčÔËķŊĩÄĘąžäΊtÃëĢŽĩąĩãPĩÚŌŧīÎŧØĩ―ĩãAĘąĢŽĩãPšÍÖąÏßlÍŽĘąÍĢÖđÔËķŊĢŪ
ĢĻ1ĢĐĩąt=ĄĄ ĄĄÃëĘąĢŽĄũPCEĘĮĩČŅüÖą―ĮČý―ĮÐÎĢŧ
ĢĻ2ĢĐĩąĩãPÔÚACąßÉÏÔËķŊĘąĢŽ―ŦĄũPEFČÆĩãEÄæĘąÕëÐýŨŠĢŽĘđĩÃĩãPĩÄķÔÓĶĩãP1ÂäÔÚEFÉÏĢŽĩãFĩÄķÔÓĶĩãΊF1ĢŽĩąEF1ĄÍABĘąĢŽĮótĩÄÖĩĢŧ
ĢĻ3ĢĐŨũĩãPđØÓÚÖąÏßEFĩÄķÔģÆĩãQĢŽÔÚÔËķŊđýģĖÖÐĢŽČôÐÎģÉĩÄËÄąßÐÎPEQFΊÁâÐÎĢŽĮótĩÄÖĩĢŧ
ĢĻ4ĢĐÔÚÕûļöÔËķŊđýģĖÖÐĢŽÉčĄũPEFĩÄÃæŧýΊSĢŽĮëÖą―ÓÐīģöSĩÄŨîīóÖĩĢŪ
Ąūīð°ļĄŋĢĻ1ĢĐ![]() ĢŧĢĻ2ĢĐt=
ĢŧĢĻ2ĢĐt=![]() ĢŧĢĻ3ĢĐĩąt=
ĢŧĢĻ3ĢĐĩąt=![]() ŧōt=
ŧōt=![]() ĘąĢŽËÄąßÐÎPEQFΊÁâÐÎĢŧĢĻ4ĢĐÔÚÕûļöÔËķŊđýģĖÖÐĢŽSĩÄŨîīóÖĩΊ12ĢŪ
ĘąĢŽËÄąßÐÎPEQFΊÁâÐÎĢŧĢĻ4ĢĐÔÚÕûļöÔËķŊđýģĖÖÐĢŽSĩÄŨîīóÖĩΊ12ĢŪ
Ąū―âÎöĄŋĘÔĖâ·ÖÎöĢšĢĻ1ĢĐÖą―ÓĀûÓÃĩČŅüÖą―ĮČý―ĮÐÎĩÄÐÔÖĘ―ĻÁĒ·―ģĖžīŋÉĢŧ
ĢĻ2ĢĐÏČĮóģöCP=![]() CEĢŽ―øķøĩÃģöCP=9Đ3tĢŽŨîšó―ĻÁĒ·―ģĖĮó―âžīŋÉĢŧ
CEĢŽ―øķøĩÃģöCP=9Đ3tĢŽŨîšó―ĻÁĒ·―ģĖĮó―âžīŋÉĢŧ
ĢĻ3ĢĐ·ÖČýÖÖĮéŋöĢŽĀûÓÃÖą―ĮČý―ĮÐÎÖÐĢŽĀûÓÃČņ―ĮČý―ĮšŊĘý―ĻÁĒ·―ģĖĮó―âžīŋÉĢŧ
ĢĻ4ĢĐ·Ö5ÖÐĮéŋöĀûÓÃČý―ĮÐÎĩÄÃæŧýđŦĘ―ĮóģöļũķÎÃæŧýÓëĘąžäĩÄšŊĘýđØÏĩĘ―ĢŽŨîšóąČ―ÏžīŋÉĩÃģö―áÂÛĢŪ
ĘÔĖâ―âÎöĢšĢĻ1ĢĐÓÉÔËķŊÖŠĢŽCE=![]() tĢŽAP=3tĢŽ
tĢŽAP=3tĢŽ
ĄßAC=9ĢŽ
ĄāPC=9Đ3tĢŽ
ĄßĄũPCEĘĮĩČŅüÖą―ĮČý―ĮÐÎĢŽ
ĄāPC=ECĢŽ
Ąā9Đ3t=![]() tĢŪ
tĢŪ
Ąāt=![]() ĢŽ
ĢŽ
đĘīð°ļΊĢš ![]() Ģŧ
Ģŧ
ĢĻ2ĢĐČįÍž1ĢŽÓÉĖâŌâĢŽĄÏPEF=ĄÏP1EF1ĢŽ
ĄßEFĄÎACĢŽĄÏC=90ĄãĢŽ
ĄāĄÏBEF=90ĄãĢŽ
ĄÏCPE=ĄÏPEFĢŽ
ĄßEF1ĄÍABĢŽ
ĄāĄÏB=ĄÏP1EF1ĢŽ
ĄāĄÏCPE=ĄÏBĢŽ
ĄātanĄÏCPE=tanB=![]() ĢŽ
ĢŽ
ĄßtanĄÏCPE=![]() ĢŽ
ĢŽ
Ąā![]() =
=![]() ĢŽ
ĢŽ
ĄāCP=![]() CEĢŽ
CEĢŽ
ĄßAP=3tĢĻ0ĢžtĢž3ĢĐĢŽCE=![]() tĢŽ
tĢŽ
ĄāCP=9Đ3tĢŽ
Ąā9Đ3t=![]() ĄÁ
ĄÁ![]() tĢŽ―âĩÃt=
tĢŽ―âĩÃt=![]() ĢŪ
ĢŪ
ĢĻ3ĢĐČįÍž2ĢŽÁŽ―ÓPQ―ŧEFÓÚĩãOĢŽ
ĄßPĄĒQđØÓÚÖąÏßEFķÔģÆĢŽ
ĄāEFīđÖąÆ―·ÖPQĢŽ
ČôËÄąßÐÎPEQFΊÁâÐÎĢŽÔōOE=OF=![]() EF
EF
ĒŲĩąĩãPÔÚACąßÉÏÔËķŊĘąĢŽ
ŌŨÖŠËÄąßÐÎPOECΊūØÐÎĢŽ
ĄāOE=PCĢŽ
ĄāPC=![]() EFĢŽ
EFĢŽ
ĄßCE=![]() tĢŽ
tĢŽ
ĄāBE=12Đ![]() tĢŽEF=BEtanB=
tĢŽEF=BEtanB=![]() ĢĻ12Đ
ĢĻ12Đ![]() tĢĐ=9ĐtĢŽ
tĢĐ=9ĐtĢŽ
Ąā9Đ3t=![]() ĢĻ9ĐtĢĐĢŽ―âĩÃt=
ĢĻ9ĐtĢĐĢŽ―âĩÃt=![]() ĢŪ
ĢŪ
ĒÚĩąĩãPÔÚCBąßÉÏÔËķŊĘąĢŽPĄĒEĄĒQČýĩãđēÏßĢŽēŧīæÔÚËÄąßÐÎPEQFĢŧ
ĒÛČįÍž3ĢŽĩąĩãPÔÚBAąßÉÏÔËķŊĘąĢŽÔōĩãPÔÚĩãBĄĒFÖŪžäĢŽ
ĄßBE=12Đ![]() tĢŽ
tĢŽ
ĄāBF=![]() ĢĻ12Đ
ĢĻ12Đ![]() tĢĐ=15Đ
tĢĐ=15Đ![]() tĢŽ
tĢŽ
ĄßBP=5ĢĻtĐ6ĢĐĢŽ
ĄāPF=BFĐBP=15Đ![]() tĐ5ĢĻtĐ6ĢĐ=45Đ
tĐ5ĢĻtĐ6ĢĐ=45Đ![]() tĢŽ
tĢŽ
ĄßĄÏPOF=ĄÏBEF=90ĄãĢŽ
ĄāPOĄÎBEĢŽ
ĄāĄÏOPF=ĄÏBĢŽ
ÔÚRtĄũPOFÖÐĢŽsinĄÏOPF=sinBĢŽ
Ąā![]() ĢŽ
ĢŽ
Ąā ĢŽ―âĩÃt=
ĢŽ―âĩÃt=![]() ĢŪ
ĢŪ
Ąāĩąt=![]() ŧōt=
ŧōt=![]() ĘąĢŽËÄąßÐÎPEQFΊÁâÐÎĢŪ
ĘąĢŽËÄąßÐÎPEQFΊÁâÐÎĢŪ
ĢĻ4ĢĐÔÚRtĄũABCÖÐĢŽļųūÝđīđÉķĻĀíĢŽĩÃĢŽBC=12ĢŽ
ĩąĩãPÔÚąßACÉÏĘąĢŽ0ĄÜtĄÜ3ĢŽ
ĩąĩãPÔÚąßBCÉÏĘąĢŽ
ĩãPšÍĩãEÖØšÏĘąĢŽ4ĢĻtĐ3ĢĐ=![]() tĢŽ
tĢŽ
Ąāt=4.5ĢŽ
ĩąPļÕšÃĩ―ĩãBĘąĢŽt=6ĢŽ
ĩąĩãPÔÚąßABÉÏĘąĢŽĮŌšÍĩãFÖØšÏĘąĢŽ
ĄßlĄÎACĢŽ
ĄāĄũBEFĄŨĄũBCAĢŽ
Ąā![]() ĢŽ
ĢŽ
Ąā![]() ĢŽ
ĢŽ
Ąā ĢŽ
ĢŽ
Ąāt=6.75ĢŽ
ĒŲĩą0ĄÜtĄÜ6ĘąĢŽČįÍž4ĢŽ

ÓÉÔËķŊÖŠĢŽCE=![]() tĢŽ
tĢŽ
ĄāBE=12Đ![]() tĢŽ
tĢŽ
ĄßEFĄÎACĢŽ
ĄāĄũBEFĄŨĄũBCAĢŽ
Ąā![]() ĢŽ
ĢŽ
Ąā ĢŽ
ĢŽ
ĄāEF=9ĐtĢŽ
ĄāSĄũPEF=![]() EFCE=
EFCE=![]() ĢĻ9ĐtĢĐĄÁ
ĢĻ9ĐtĢĐĄÁ![]() t=Đ
t=Đ![]() ĢĻtĐ
ĢĻtĐ![]() ĢĐ2+
ĢĐ2+![]() ĢŽ
ĢŽ
īËĘąĩąt=3ĘąĢŽSĄũPEFŨîīó=Đ![]() ĢĻ3Đ
ĢĻ3Đ![]() ĢĐ2+
ĢĐ2+![]() =12ĢŽ
=12ĢŽ
ĒÚĩą3ĢžtĢž4.5ĘąĢŽČįÍž5ĢŽ
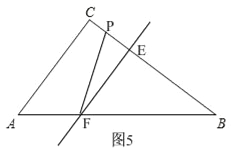
ÓÉÔËķŊÖŠĢŽPE=![]() tĐ4ĢĻtĐ3ĢĐ=Đ
tĐ4ĢĻtĐ3ĢĐ=Đ![]() t+12ĢŽ
t+12ĢŽ
ĄāSĄũPEF=![]() EFPE=
EFPE=![]() ĢĻ9ĐtĢĐĢĻĐ
ĢĻ9ĐtĢĐĢĻĐ![]() t+12ĢĐ=
t+12ĢĐ=![]() t2Đ18t+54ĢŽ
t2Đ18t+54ĢŽ
īËĘąēŧīæÔÚŨîīóÖĩĢŽ
ĒÛĩą4.5ĢžtĄÜ6ĘąĢŽČįÍž6ĢŽ

ÍŽĒÚĩÄ·―·ĻĢŽĩÃĢŽSĄũPEF=Đ![]() t2+18tĐ54=Đ
t2+18tĐ54=Đ![]() ĢĻtĐ
ĢĻtĐ![]() ĢĐ2+
ĢĐ2+![]()
īËĘąĢŽĩąt=6ĘąĢŽSĄũPEFŨîīó=6ĢŽ
ĒÜĩą6ĢžtĢž6.75ĘąĢŽČįÍž7ĢŽ

ÔÚRtĄũABCÖÐĢŽsinĄÏB=![]() =
=![]() ĢŽ
ĢŽ
ÔÚRtĄũBEQÖÐĢŽsinĄÏB= =
=![]() ĢŽ
ĢŽ
ĄāQE=![]() ĢĻ36Đ4tĢĐĢŽÔÚRtĄũBEFÖÐĢŽsinĄÏB=
ĢĻ36Đ4tĢĐĢŽÔÚRtĄũBEFÖÐĢŽsinĄÏB=![]() =
=![]() ĢŽ
ĢŽ
ĄāBF=![]() ĢĻ9ĐtĢĐĢŽ
ĢĻ9ĐtĢĐĢŽ
ĄāPF=BFĐBP=![]() ĢĻ9ĐtĢĐĐ5ĢĻtĐ6ĢĐ=45Đ
ĢĻ9ĐtĢĐĐ5ĢĻtĐ6ĢĐ=45Đ![]() t
t
SĄũPEF=![]() PFQE=
PFQE=![]() t2Đ42t+162ĢŽ
t2Đ42t+162ĢŽ
īËĘąēŧīæÔÚŨîīóÖĩĢŧ
ĒÝĩą6.75ĢžtĢž9ĘąĢŽČįÍž8ĢŽ

ÍŽĒÜĩÄ·―·ĻĢŽĩÃĢŽSĄũPEF=Đ![]() t2+42tĐ162ĢŽ
t2+42tĐ162ĢŽ
ÓÉÓÚķÔģÆÖát=![]() Ģū9ĢŽ
Ģū9ĢŽ
ĄāīËʹȥēŧĩ―ŨîīóÖĩĢŽ
ĄāÔÚÕûļöÔËķŊđýģĖÖÐĢŽSĩÄŨîīóÖĩΊ12ĢŪ




ĄūĖâÄŋĄŋΊÁËÆÕž°ŧ·ąĢÖŠĘķĢŽÔöĮŋŧ·ąĢŌâĘķĢŽÄģÖÐŅ§ŨéÖŊÁËŧ·ąĢÖŠĘķūšČüŧîķŊĢŽģõÖÐČýļöÄęžķļųūÝģõČüģÉžĻ·ÖąðŅĄģöÁË10ÃûÍŽŅ§ēΞÓūöČüĢĻÂú·ÖΊ100·ÖĢĐČįąíËųĘūĢš
ūöČüģÉžĻĢĻĩĨÎŧĢš·ÖĢĐ
ĢĻ1ĢĐĮëÄãĖîÐīÏÂąíĢš
Æ―ūųĘý | ÖÚĘý | ÖÐÎŧĘý | |
ÆßÄęžķ | 85.5 | 87 | |
°ËÄęžķ | 85.5 | 85 | |
ūÅÄęžķ | 84 |
ĢĻ2ĢĐĮëīÓŌÔÏÂÁ―ļöēŧÍŽĩÄ―ĮķČķÔČýļöÄęžķĩÄūöČüģÉžĻ―øÐзÖÎöĢš
īÓÆ―ūųĘýšÍÖÚĘýÏā―ášÏŋīĢĻ·ÖÎöÄÄļöÄęžķģÉžĻšÃÐĐĢĐĢšĢŧ
īÓÆ―ūųĘýšÍÖÐÎŧĘýÏā―ášÏŋīĢĻ·ÖÎöÄÄļöÄęžķģÉžĻšÃÐĐĢĐĢšĢŧ
ĢĻ3ĢĐČįđûÔÚÃŋļöÄęžķēΞÓūöČüĩÄŅĄĘÖÖÐ·ÖąðŅĄģöČýČËēΞÓūöČüĢŽÄãČÏΊÄÄļöÄęžķĩÄĘĩÁĶļüĮŋŌŧÐĐĄĢËĩÃũĀíÓÉĢšĄĢ
ĄūĖâÄŋĄŋÍøÉÏđšÎïŌŅūģÉΊČËÃĮģĢÓÃĩÄŌŧÖÖđšÎï·―Ę―ĢŽĘÛšóÆĀžÛĖØąðŌýČËđØŨĒĢŽÎŠÁË―âĘÐÃņķÔĘÛšóÆĀžÛĩÄđØŨĒĮéŋöĢŽËæŧúēÉ·Ãēŋ·ÖĘÐÃņĢŽķÔēÉ·ÃĮéŋöÖÆŨũÁËČįÏÂÍģžÆÍžąíĢš
đØŨĒĮéŋö | ÆĩĘý | ÆĩÂĘ |
AĢŪļßķČđØŨĒ | 50 | b |
BĢŪŌŧ°ãđØŨĒ | 120 | 0.6 |
CĢŪēŧđØŨĒ | a | 0.1 |
DĢŪēŧÖŠĩĀ | 10 | 0.05 |
ĢĻ1ĢĐļųūÝÉÏĘöÍģžÆÍžŋÉĩÃīËīÎēÉ·ÃĩÄČËĘýΊĄĄ ĄĄČËĢŽa=ĄĄ ĄĄĢŽb=ĄĄ ĄĄĢŧ
ĢĻ2ĢĐļųūÝŌÔÉÏÐÅÏĒēđČŦĖõÐÎÍģžÆÍžĢŧ
ĢĻ3ĢĐļųūÝÉÏĘöēÉ·Ã―áđûĢŽĮëđĀžÆÔÚ6400ÃûĘÐÃņÖÐĢŽļßķČđØŨĒĘÛšóÆĀžÛĩÄĘÐÃņÔžÓÐķāÉŲČËĢŋ


