题目内容
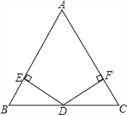
【题目】感知:如图1,在△ABC中,∠ABC=42°,∠ACB=72°,点D是AB上一点,E是AC上一点,BE、CD相交于点F.
(1)若∠ACD=35°,∠ABE=20°,求∠BFC的度数;
(2)若CD平分∠ACB,BE平分∠ABC,求∠BFC的度数;
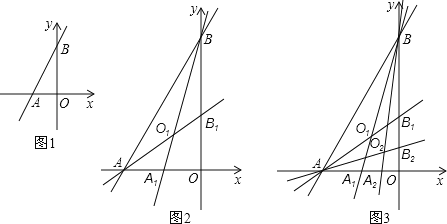
探究:如图2,在△ABC中,BE平分∠ABC,CD平分∠ACB,写出∠BFC与∠A之间的数量关系,并说明理由;
应用:如图3,在△ABC中,BD平分∠ABC ,CD平分外角∠ACE,请直接写出∠BDC与∠A之间的数量关系.



【答案】(1)121°;(2)∠BFC=90°+![]() ∠A,证明见解析;(3)∠BDC=
∠A,证明见解析;(3)∠BDC=![]() ∠A.
∠A.
【解析】分析:(1)、根据△ABC的内角和定理得出∠A的度数,然后根据∠BEC=∠A+∠ABE得出答案;(2)、根据角平分线的性质得出∠ABE=![]() ∠ABC,∠ACD=
∠ABC,∠ACD=![]() ∠ACB,最后根据三角形外角的性质以及三角形内角和定理得出答案;(3)、根据三角形外角的性质以及三角形内角和定理得出答案.
∠ACB,最后根据三角形外角的性质以及三角形内角和定理得出答案;(3)、根据三角形外角的性质以及三角形内角和定理得出答案.
详解:(1)、∵在△ABC中,∠ABC+∠ACB+∠A=180°,又∵∠ABC=42°,∠ACB=72°,
∴∠A=66°, ∵∠BEC=∠A+∠ABE=20°+66°=86°,
又∵∠BFC=∠ACD+∠BEC=35°+86°=121°;
(2)、结论:∠BFC=90°+![]() ∠A,
∠A,
证明:∵BE平分∠ABC,CD平分∠ACB, ∴∠ABE=![]() ∠ABC,∠ACD=
∠ABC,∠ACD=![]() ∠ACB,
∠ACB,
∵∠BEC=∠A+∠ABE,∠BFC=∠ACD+∠BEC, ∴∠BFC=∠A+∠ACD+∠ABE,
∴∠BFC=∠A+![]() ∠ABC+
∠ABC+![]() ∠ACB, ∵∠A+∠ABC+∠ACB=180°,
∠ACB, ∵∠A+∠ABC+∠ACB=180°,
∴∠BFC=90°+![]() ∠A;
∠A;
(3)∠BDC=![]() ∠A.
∠A.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目