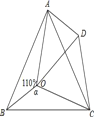
题目内容
【题目】![]() 中,
中,![]() ,
,![]() 为高线,点
为高线,点![]() 在边
在边![]() 上,且
上,且![]() ,连接
,连接![]() ,
,![]() ,与边
,与边![]() 相交于点
相交于点![]() .
.
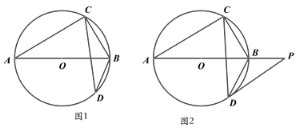
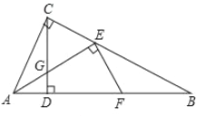
(1)如图1,当![]() 时,求证:
时,求证:![]()
(2)如图2,当![]() 时,则线段
时,则线段![]() 、
、![]() 的数量关系为 ;
的数量关系为 ;
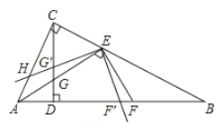
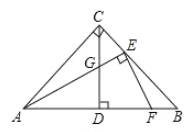
(3)如图3,在(2)的条件下,将![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() ,旋转后
,旋转后![]() 边所在的直线与边
边所在的直线与边![]() 相交于点
相交于点![]() ,
,![]() 边所在的直线与边
边所在的直线与边![]() 相交于点
相交于点![]() ,与高线
,与高线![]() 相交于点
相交于点![]() ,若
,若![]() ,且
,且![]() ,求线段
,求线段![]() H的长.
H的长.
【答案】(1)证明见解析;(2)当![]() 时,
时,![]() ;(3)2
;(3)2![]()
【解析】
(1)根据tan∠BAC=1=tan45°,得出△ABC为等腰直角三角形,再过E点作EK⊥BC,EK与CD相交于点K,得出∠GKE=45°=∠B,再根据∠GEK+∠KEF=90°=∠KEF+∠BEF,得出△GEK∽△FEB,从而证出![]() ,即可得出EF=2EG;
,即可得出EF=2EG;
(2)根据(1)的证明过程,同理可证出当tan∠BAC=2时,得出EF=EG;
(3)根据(2)的结论,先设AC=3k,得出BC=6k,EC=![]() EC=2k,再过点E作EM⊥BC,EM与CD的延长线相交于点M,得出△AGC∽△EGM,得出
EC=2k,再过点E作EM⊥BC,EM与CD的延长线相交于点M,得出△AGC∽△EGM,得出![]() ,再过点G作GN∥EH,与AH相交于点N,得出△ANG∽△AHE,得出NH的值,同理得出△GEM∽△FEB,得出EF=EG.同理可证EF′=EG′,∠FEF'=∠GEG',得出△GEG'≌△FEF',即可证出
,再过点G作GN∥EH,与AH相交于点N,得出△ANG∽△AHE,得出NH的值,同理得出△GEM∽△FEB,得出EF=EG.同理可证EF′=EG′,∠FEF'=∠GEG',得出△GEG'≌△FEF',即可证出![]() 的值,再根据HG′∥NG,同理可证
的值,再根据HG′∥NG,同理可证![]() ,得出EC=CH,得出△HCE是等腰直角三角形,在△HG'C中,求出CW的值,从而得出G′H的值.
,得出EC=CH,得出△HCE是等腰直角三角形,在△HG'C中,求出CW的值,从而得出G′H的值.
(1)证明:在![]() 中,
中, ![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
![]() 为等腰直角三角形,
为等腰直角三角形,
![]() ,
,
![]() ,
,
过![]() 点作
点作![]() ,
,![]() 与
与![]() 相交于点
相交于点![]() ,
,
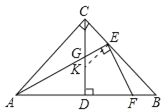
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ;
;
(2)根据(1)的证明,同理可证:
当![]() 时,
时,![]() ;
;
(3)在![]() 中,
中, ![]() ,
,![]() ,
,
则![]() ,
,
设![]() ,则BC=6k,则
,则BC=6k,则![]() ,
,
过点![]() 作
作![]() ,
,![]() 与
与![]() 的延长线相交于点
的延长线相交于点![]() ,
, ![]() ,
,
![]() .
.
在![]() 与
与![]() 中,
中,
![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
![]()
过点![]() 作
作![]() ,与
,与![]() 相交于点
相交于点![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,![]()
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
同理可证![]() ,
, ![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
![]() ,同理可证
,同理可证![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() 是等腰直角三角形,
是等腰直角三角形,![]() ,
,
在![]() 中,过点
中,过点![]() 作
作![]() ,垂足是
,垂足是![]() ,
,
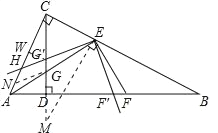
设![]() ,则HW=x,则
,则HW=x,则![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.

 优学名师名题系列答案
优学名师名题系列答案