题目内容
如图,在?ABCD中,BC=4,AB=2,点E、F分别是BC、AD的中点.
(1)求证:△ABE≌△CDF;
(2)当四边形AECF为菱形时,求AC的长.

(1)求证:△ABE≌△CDF;
(2)当四边形AECF为菱形时,求AC的长.

(1)证明:∵四边形ABCD是平行四边形,
∴AB=CD,∠B=∠D,AD=BC,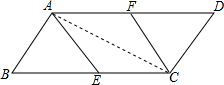
∵点E、F分别是BC、AD的中点,
∴DF=
AD,BE=
BC,
∴DF=BE,
在△ABE和△CDF中,
,
∴△ABE≌△CDF(SAS);
(2)连接AC,
∵在?ABCD中,BC=4,AB=2,点E、F分别是BC、AD的中点,
∴BE=CE=2,
∴AB=BE,
∵四边形AECF为菱形,
∴AE=EC,AE∥CF,
∴AB=BE=AE,
∴∠B=∠AEB=60°,
∴∠ECF=⊙AEB=60°,
∴∠ACE=
∠ECF=30°,
∴∠BAC=180°-∠B-∠ACE=90°,
∴AC=
=2
.
∴AB=CD,∠B=∠D,AD=BC,

∵点E、F分别是BC、AD的中点,
∴DF=
| 1 |
| 2 |
| 1 |
| 2 |
∴DF=BE,
在△ABE和△CDF中,
|
∴△ABE≌△CDF(SAS);
(2)连接AC,
∵在?ABCD中,BC=4,AB=2,点E、F分别是BC、AD的中点,
∴BE=CE=2,
∴AB=BE,
∵四边形AECF为菱形,
∴AE=EC,AE∥CF,
∴AB=BE=AE,
∴∠B=∠AEB=60°,
∴∠ECF=⊙AEB=60°,
∴∠ACE=
| 1 |
| 2 |
∴∠BAC=180°-∠B-∠ACE=90°,
∴AC=
| BC2-AB2 |
| 3 |

练习册系列答案
 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案
相关题目






