题目内容
如图，在?ABCD中，BC=2AB，E为BC的中点，试说明AE⊥DE．
证明：∵平行四边形ABCD，
∴AB∥CD，AB=CD，
∴∠B+∠C=180°，
∵BC=2AB，E为BC的中点，
∴AB=BE=CE=CD，
∴∠BAE=∠AEB，∠CED=∠CDE，
∵∠B+∠BAE+∠AEB=180°，∠C+∠CDE+∠CED=180°，
∴2∠BEA+2∠CED=360°-180°=180°，
∴∠AEB+∠CED=90°，
∴∠AED=90°，
∴AE⊥DE．
∴AB∥CD，AB=CD，
∴∠B+∠C=180°，
∵BC=2AB，E为BC的中点，
∴AB=BE=CE=CD，
∴∠BAE=∠AEB，∠CED=∠CDE，
∵∠B+∠BAE+∠AEB=180°，∠C+∠CDE+∠CED=180°，
∴2∠BEA+2∠CED=360°-180°=180°，
∴∠AEB+∠CED=90°，
∴∠AED=90°，
∴AE⊥DE．
练习册系列答案
相关题目
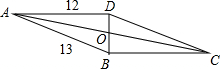
点A、B、C构成平行四边形的顶点，求点D的坐标．