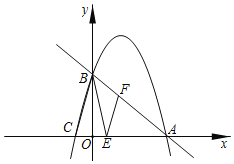
题目内容
【题目】如图,抛物线![]() 经点
经点![]() ,与
,与![]() 轴相交于点
轴相交于点![]() .
.
(1)求抛物线的解析式;
(2)定义:平面上的任一点到二次函数图象上与它横坐标相同的点的距离,称为点到二次函数图象的垂直距离.如:点![]() 到二次函数图象的垂直距离是线段
到二次函数图象的垂直距离是线段![]() 的长.已知点
的长.已知点![]() 为抛物线对称轴上的一点,且在
为抛物线对称轴上的一点,且在![]() 轴上方,点
轴上方,点![]() 为平面内一点,当以
为平面内一点,当以![]() 为顶点的四边形是边长为4的菱形时,请求出点
为顶点的四边形是边长为4的菱形时,请求出点![]() 到二次函数图象的垂直距离.
到二次函数图象的垂直距离.
(3)在(2)中,当点![]() 到二次函数图象的垂直距离最小时,在
到二次函数图象的垂直距离最小时,在![]() 为顶点的菱形内部是否存在点
为顶点的菱形内部是否存在点![]() ,使得
,使得![]() 之和最小,若存在,请求出最小值;若不存在,请说明理由.
之和最小,若存在,请求出最小值;若不存在,请说明理由.
【答案】(1)![]() ;(2)
;(2)![]() 或
或![]() ;(3)
;(3)![]() 的和最小值为
的和最小值为![]() .
.
【解析】
(1)利用待定系数法列方程组求出a、b的值即可;(2)根据抛物线解析式可求出A、B两点坐标,即可得出对称轴解析式,分两种情况:当以AB为边时,EF//AB,由对称轴可得E点的横坐标,根据EF=AB=4即可得出F点的横坐标,根据菱形的性质求出EM的长,把F点横坐标代入抛物线解析式,根据点到二次函数图象的垂直距离的定义即可得出答案;当以AB为菱形对角线时,根据菱形的性质可得AB⊥EF,利用勾股定理可求出FM的长,进而可得F点坐标,把F点横坐标代入抛物线解析式,根据点到二次函数图象的垂直距离的定义即可得出答案;(3)由当![]() 时,点
时,点![]() 到二次函数图象的垂直距离最小,将
到二次函数图象的垂直距离最小,将![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 到
到![]() 位置,连接
位置,连接![]() ,作
,作![]() 于
于![]() ,根据AB=AF=BF可证明△ABF是等边三角形,根据旋转性质可知
,根据AB=AF=BF可证明△ABF是等边三角形,根据旋转性质可知![]() 均为等边三角形,进而可得当
均为等边三角形,进而可得当![]() 共线时
共线时![]() 的和最短,在Rt△APN中,利用勾股定理求出AN的长即可得答案.
的和最短,在Rt△APN中,利用勾股定理求出AN的长即可得答案.
(1)∵抛物线![]() 过点
过点![]() ,
,
∴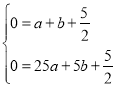
解得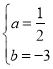
∴解析式![]() .
.
(2)当![]() 时,由
时,由![]() ,得
,得![]() ,
,
对称轴所在直线为![]() ,顶点坐标为
,顶点坐标为![]() ,
,
∵抛物线与![]() 轴相交于点
轴相交于点![]() .
.
∴![]()
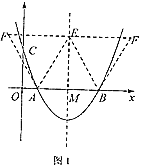
①若![]() 为菱形的边,如图1,则
为菱形的边,如图1,则![]() ,且
,且![]() 的横坐标为3
的横坐标为3
∴![]() 的横坐标为7或-1,
的横坐标为7或-1,
∵![]() ,
,
∴![]()
∴![]() 或
或![]() ,
,
当![]() ,
,
∴点![]() 到二次函数图象的垂直距离为
到二次函数图象的垂直距离为![]() ,
,
当x=-1时,y=![]() ×(-1)2-(-1)×3+
×(-1)2-(-1)×3+![]() =6,
=6,
∴点![]() 到二次函数图象的垂直距离为
到二次函数图象的垂直距离为![]() .
.
②若![]() 为对角线,如图2,
为对角线,如图2,
∵![]() 是菱形,
是菱形,![]() ,
,
∴EM=FM=![]() =
=![]()
∴![]() ,
,
当x=3时,y=![]() ×32-3×3+
×32-3×3+![]() =-2,
=-2,
∴点![]() 到二次函数图象的垂直距离为
到二次函数图象的垂直距离为![]() =
=![]() -2,
-2,
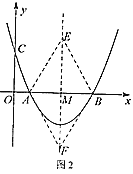
综上所述:点![]() 到二次函数图象的垂直距离为
到二次函数图象的垂直距离为![]() 或
或![]() -2.
-2.
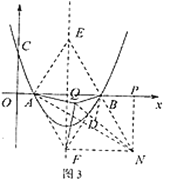
(3)当![]() 时,点
时,点![]() 到二次函数图象的垂直距离最小,如图3,将
到二次函数图象的垂直距离最小,如图3,将![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 到
到![]() 位置,连接
位置,连接![]() ,作
,作![]() 于
于![]() ,
,
∵AB=4,AF=BF=4,
∴△ABF是等边三角形,
∵将![]() 绕
绕![]() 逆时针旋转
逆时针旋转![]() 到
到![]() 位置,
位置,
∴![]() ≌
≌![]() ,且
,且![]() 均为等边三角形,
均为等边三角形,
∴![]() ,
,
∵![]() ,
,
∴当![]() 共线时
共线时![]() 的和最短,即最短值为
的和最短,即最短值为![]() 的长.
的长.
∵![]() ,
,
∴![]() 且
且![]() ,
,
∴![]() ,
,
∴![]() ,
,
在![]() 中,
中,![]() ,
,
∴![]() 的和最小值为
的和最小值为![]() .
.

 高中必刷题系列答案
高中必刷题系列答案【题目】商场里某产品每月销售量y(只)与销售单价x(元)满足一次函数关系,经调查部分数据如表:(已知每只进价为10元,每只利润=销售单价-进价)
销售单价x(元) | 21 | 23 | 25 | … |
月销售额y(只) | 29 | 27 | 25 | … |
(1)求出y与x之间的函数表达式;
(2)这产品每月的总利润为w元,求w关于x的函数表达式,并指出销售单价为多少元时利润最大,最大利润是多少元?
(3)由于该产品市场需求量较大,进价在原有基础上提高了a元(a<10),但每月销售量与销售价仍满足上述一次函数关系,此时,随着销售量的增大,所得的最大利润比(2)中的最大利润减少了144元,求a的值.