题目内容
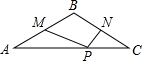 如图,在等腰三角形ABC中,∠ABC=120°,点P是底边AC上一个动点,M、N分别是AB、BC的中点,若PM+PN的最小值为4,则△ABC的周长是
如图,在等腰三角形ABC中,∠ABC=120°,点P是底边AC上一个动点,M、N分别是AB、BC的中点,若PM+PN的最小值为4,则△ABC的周长是分析:本题首先要明确P点在何处,通过M关于AC的对称点M′,根据勾股定理就可求出MN的长,根据中位线的性质及三角函数分别求出AB、BC、AC的长,从而得到△ABC的周长.
解答:解:作M点关于AC的对称点M′,连接M'N,则与AC的交点即是P点的位置,
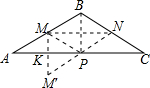 ∵M,N分别是AB,BC的中点,
∵M,N分别是AB,BC的中点,
∴MN是△ABC的中位线,
∴MN∥AC,
∴
=
=1,
∴PM′=PN,
即:当PM+PN最小时P在AC的中点,
∴MN=
AC
∴PM=PN=2,MN=2
∴AC=4
,
AB=BC=2PM=2PN=4,
∴△ABC的周长为:4+4+4
=8+4
.
故答案为:8+4
.
 ∵M,N分别是AB,BC的中点,
∵M,N分别是AB,BC的中点,∴MN是△ABC的中位线,
∴MN∥AC,
∴
| PM′ |
| PN |
| KM′ |
| KM |
∴PM′=PN,
即:当PM+PN最小时P在AC的中点,
∴MN=
| 1 |
| 2 |
∴PM=PN=2,MN=2
| 3 |
∴AC=4
| 3 |
AB=BC=2PM=2PN=4,
∴△ABC的周长为:4+4+4
| 3 |
| 3 |
故答案为:8+4
| 3 |
点评:本题考查等腰三角形的性质和轴对称及三角函数等知识的综合应用.正确确定P点的位置是解题的关键.

练习册系列答案
 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案
相关题目
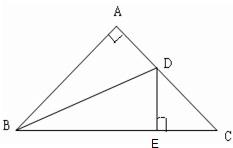 24、已知:如图,在等腰三角形ABC中,∠A=90°,∠ABC的平分线BD与AC交于点D,DE⊥BC于点E.求证:AD=CE.
24、已知:如图,在等腰三角形ABC中,∠A=90°,∠ABC的平分线BD与AC交于点D,DE⊥BC于点E.求证:AD=CE.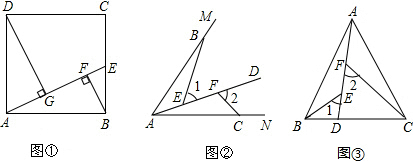
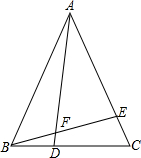 如图,在等腰三角形ABC中,AB=AC=12,BC=8,又BD=3,CE=2.
如图,在等腰三角形ABC中,AB=AC=12,BC=8,又BD=3,CE=2.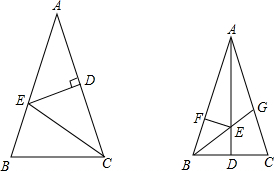 (1)如图,在等腰三角形ABC中,AB=AC,AD是BC边上的中线,∠ABC的平分线BG,交AD于点E,EF⊥AB,垂足为F.
(1)如图,在等腰三角形ABC中,AB=AC,AD是BC边上的中线,∠ABC的平分线BG,交AD于点E,EF⊥AB,垂足为F.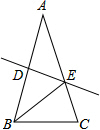 如图,在等腰三角形ABC中,AB=AC,∠A=40°,线段AB的垂直平分线交AB于点D,交AC于点E,连接BE,则∠CBE等于( )
如图,在等腰三角形ABC中,AB=AC,∠A=40°,线段AB的垂直平分线交AB于点D,交AC于点E,连接BE,则∠CBE等于( )