Question

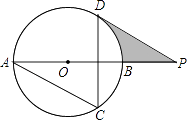
【题目】如图，△ABC内接于⊙O，AB是⊙O的直径，∠BAC=2∠B，⊙O的切线AP与OC的延长线相交于点P，若PA= cm，求AC的长．

Answer 1

【答案】解：∵AB是⊙O直径， ∴∠ACB=90°，
∵∠BAC=2∠B，
∴∠B=30°，∠BAC=60°，
∵OA=OC，
∴△AOC是等边三角形，
∴∠AOC=60°，AC=OA，
∵PA是⊙O切线，
∴∠OAP=90°，
在Rt△OAP中，PA=6 cm，∠AOP=60°，
∴OA= = =6cm，
∴AC=OA=6cm
【解析】根据直径求出∠ACB=90°，求出∠B=30°，∠BAC=60°，得出△AOC是等边三角形，得出∠AOC=60°，OA=AC， 在Rt△OAP中，求出OA，即可求出答案．
【考点精析】根据题目的已知条件，利用切线的性质定理的相关知识可以得到问题的答案，需要掌握切线的性质：1、经过切点垂直于这条半径的直线是圆的切线2、经过切点垂直于切线的直线必经过圆心3、圆的切线垂直于经过切点的半径．