题目内容
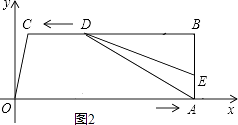
【题目】如图，在四边形OABC中，OA∥BC，∠OAB=90°，O为原点，点C的坐标为（2，8），点A的坐标为（26，0），点D从点B出发，以每秒1个单位长度的速度沿BC向点C运动，点E同时从点O出发，以每秒3个单位长度的速度沿折线OAB运动，当点E达到点B时，点D也停止运动，从运动开始，设D（E）点运动的时间为t秒．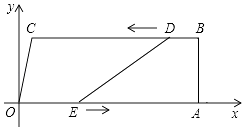
（1）当t为何值时，四边形ABDE是矩形；
（2）当t为何值时，四边形OEDC是平行四边形？
（3）连接AD，记△ADE的面积为S，求S与t的函数关系式．
【答案】
（1）解：∵点C的坐标为（2，8），点A的坐标为（26，0），
∴OA=26，BC=24，AB=8，
∵D（E）点运动的时间为t秒，
∴BD=t，OE=3t，
∵四边形ABDE是矩形，
∴BD=AE，
即t=26﹣3t，
解得，t= 
；
（2）解：∵四边形OEDC为平行四边形，
∴CD=OE，
即24﹣t=3t，
解得，t=6；
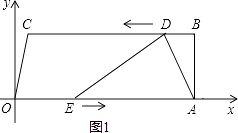
（3）解：如图1，当点E在OA上时，
AE=26﹣3t，
则S= 
×AE×AB= ×（26﹣3t）×8=﹣12t+104，
当点E在AB上时，AE=3t﹣26，BD=t，
则S= ×AE×DB= ×（3t﹣26）×t= t2﹣13t．
【解析】（1）根据矩形的判定定理列出关系式，计算即可；（2）根据平行四边形的判定定理和性质定理解答；（3）分点E在OA上和点E在AB上两种情况，根据三角形的面积公式计算即可
【考点精析】本题主要考查了三角形的面积和平行四边形的判定的相关知识点，需要掌握三角形的面积=1/2×底×高；两组对边分别平行的四边形是平行四边形：两组对边分别相等的四边形是平行四边形；一组对边平行且相等的四边形是平行四边形；两组对角分别相等的四边形是平行四边形；对角线互相平分的四边形是平行四边形才能正确解答此题．
