��Ŀ����
����Ŀ�����������![]() �Ķ�����������
�Ķ�����������![]() �ϣ�ͬʱ��������
�ϣ�ͬʱ��������![]() �Ķ�����������
�Ķ�����������![]() �ϣ���ô�����dz�������
�ϣ���ô�����dz�������![]() ��
��![]() ������
������
��1����֪������![]() ���ж����������ߣ���
���ж����������ߣ���![]() ����
����![]()
![]() ����֪�������Ƿ��������˵�����ɣ�
����֪�������Ƿ��������˵�����ɣ�
��2����֪������![]() :
: ![]() ����P������Ϊ
����P������Ϊ![]() �����������Ƶ�
�����������Ƶ�![]() ��ת180��õ�������
��ת180��õ�������![]() ���˴����dzƵ�PΪ��ת�㣩����������
���˴����dzƵ�PΪ��ת�㣩����������![]() ��
��![]() ��������������
��������������![]() �Ľ���ʽ��
�Ľ���ʽ��
��3���ڣ�2���������£���֪��![]() ��������
��������![]() �ϵ�һ�㣬���Ե�AΪ���㲢��������
�ϵ�һ�㣬���Ե�AΪ���㲢��������![]() �������������
�������������![]() �Ľ���ʽ�����жϴ�ʱ������
�Ľ���ʽ�����жϴ�ʱ������![]() �ܷ���������
�ܷ���������![]() ��ת���������ܣ��������ת�����ꣻ�����ܣ���˵��������ɣ�
��ת���������ܣ��������ת�����ꣻ�����ܣ���˵��������ɣ�
��4�����������۲��룺����������![]() ������������ǵĶ���ʽ��ϵ�����ֱ��Ϊ
������������ǵĶ���ʽ��ϵ�����ֱ��Ϊ![]() ��Ӧ����������ϵ�� ��
��Ӧ����������ϵ�� ��
�ο���ʽ���е����깫ʽ��������![]() �����߶�AB���е�����Ϊ
�����߶�AB���е�����Ϊ![]() ��
��
���𰸡���1�������ߢ�����֪��������������������ߢڲ�����֪����������������ɼ���������2��������![]() ��
�� ![]() ��
��![]() ����3����ת��
����3����ת��![]() ����4��
����4��![]() ��
��
�������������������1��������������ߢ������Ķ������꣬Ȼ����ݶ���������߹����������ɽ����жϣ�
��2�������������C1�Ķ������꣬��C2����Ϊ��x,y��,������ת��֪������C2�Ķ�����C1�Ķ�����ڵ�P(t��-1)�Գƣ��Ӷ����ú�t�Ĵ���ʽ��ʾC2�Ķ������꣬Ȼ����ݶ������C1�Ľ���ʽ��ȷ����C2�Ķ��㣬�Ӷ������C2�Ľ���ʽ��
��3�������������A�����꣬�Ӷ������ö���ʽ��ȷ��C2�Ľ���ʽ���Ӷ���ȷ������ת������ꣻ
��4�����ݶ������������������ϵ����Ϊ�෴�����Ӷ��ɵ�.
�����������1����֪������![]() ����������Ϊ
����������Ϊ![]() ��
��
�����ߢ�![]() ����������Ϊ
����������Ϊ![]() ��
��
�����ߢ�![]() ����������Ϊ
����������Ϊ![]() ��
��
�����Ե�![]() �������ߢ�
�������ߢ�![]() �ϣ��ҵ�
�ϣ��ҵ�![]() Ҳ����֪������
Ҳ����֪������
![]() �ϣ�����
�ϣ�����![]() ��������֪������
��������֪������![]() �ϣ�
�ϣ�
�������ߢ�����֪��������������������ߢڲ�����֪�������������
��2��������![]() :
: ![]() ����������Ϊ
����������Ϊ![]() ��
��
��������![]() �Ķ�������Ϊ
�Ķ�������Ϊ![]() �������е����깫ʽ��
�������е����깫ʽ�� 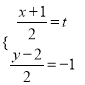 ��
��
��ã� ![]() ����
����![]() ����������
����������![]() ��
��
���� ![]() ����ã�t��0��t��2��
����ã�t��0��t��2��
��������![]() �Ķ�������Ϊ
�Ķ�������Ϊ![]() ��
��![]() ��
��
��������![]() ��������
��������![]() ���ڴ�С��ͬ���������෴��
���ڴ�С��ͬ���������෴��
��������![]() ��
�� ![]() ��
��![]() ��
��
��������![]() ��
�� ![]() ��
��![]() ��
��
��3����![]() ����������
����������![]() ���ã�
���ã� ![]() ����
����![]() ��
��
��������![]() ��
�� ![]() ����������
����������![]() �Ķ���
�Ķ���![]() ���룬
���룬
��ã� ![]() ����ʱ������
����ʱ������![]() ��
�� ![]() ����
����![]() ��
��
���������߿��ڴ�С��ͬ���������෴����������![]() �ܷ���������
�ܷ���������![]() ��ת������
��ת������
��ת��Ϊ������![]() ��
��![]() ���е㣬��
���е㣬��![]() ��
��
��4��![]() ��
��