题目内容
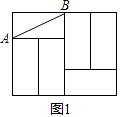
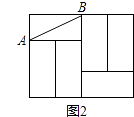
【题目】如图,正方形ABCD和正方形CEFG中,点D在CG上,BC=1,CE=3,H是AF的中点,那么CH的长是 . 
【答案】![]()
【解析】解:∵正方形ABCD和正方形CEFG中,点D在CG上,BC=1,CE=3,
∴AB=BC=1,CE=EF=3,∠E=90°,
延长AD交EF于M,连接AC、CF,

则AM=BC+CE=1+3=4,FM=EF﹣AB=3﹣1=2,∠AMF=90°,
∵四边形ABCD和四边形GCEF是正方形,
∴∠ACD=∠GCF=45°,
∴∠ACF=90°,
∵H为AF的中点,
∴CH= ![]() AF,
AF,
在Rt△AMF中,由勾股定理得:AF= ![]() =
= ![]() =2
=2 ![]() ,
,
∴CH= ![]() ,
,
故答案为: ![]() .
.
根据正方形的性质求出AB=BC=1,CE=EF=3,∠E=90°,延长AD交EF于M,连接AC、CF,求出AM=4,FM=2,∠AMF=90°,根据正方形性质求出∠ACF=90°,根据直角三角形斜边上的中线性质求出CH= ![]() AF,根据勾股定理求出AF即可.
AF,根据勾股定理求出AF即可.

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案 应用题作业本系列答案
应用题作业本系列答案
相关题目