题目内容
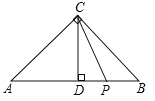
【题目】如图,在△ABC中,∠ACB=90°,∠A=45°,CD⊥AB于点D,点P在线段DB上,若AP2-PB2=48,则△PCD的面积为____.
【答案】6
【解析】
根据等角对等边,可得AC=BC,由等腰三角形的“三线合一”可得AD=BD=![]() AB,利用直角三角形斜边的中线等于斜边的一半,可得CD=
AB,利用直角三角形斜边的中线等于斜边的一半,可得CD=![]() AB,由AP2-PB2=48,利用平方差公式及线段的和差公式将其变形可得CD·PD=12,利用△PCD的面积 =
AB,由AP2-PB2=48,利用平方差公式及线段的和差公式将其变形可得CD·PD=12,利用△PCD的面积 =![]() CD·PD可得.
CD·PD可得.
解:∵ 在△ABC中,∠ACB=90°,∠A=45°,
∴∠B=45°,
∴AC=BC,
∵CD⊥AB,
∴AD=BD=CD=![]() AB,
AB,
∵AP2-PB2=48,
∴(AP+PB)(AP-PB)=48,
∴AB(AD+PD-BD+DP)=48,
∴AB·2PD=48,
∴2CD·2PD=48,
∴CD·PD=12,
∴ △PCD的面积=![]() CD·PD=6.
CD·PD=6.
故答案为:6.

练习册系列答案
相关题目