题目内容
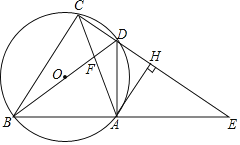
【题目】如图1,在△ABC中,AB=AC=20,tanB=![]() ,点D为BC边上的动点(D不与点B,C重合).以D为顶点作∠ADE=∠B,射线DE交AC边于点E,过点A作AF⊥AD交射线DE于点F,连接CF.
,点D为BC边上的动点(D不与点B,C重合).以D为顶点作∠ADE=∠B,射线DE交AC边于点E,过点A作AF⊥AD交射线DE于点F,连接CF.
(1)求证:△ABD∽△DCE;
(2)当DE∥AB时(如图2),求AE的长;
(3)点D在BC边上运动的过程中,是否存在某个位置,使得DF=CF?若存在,求出此时BD的长;若不存在,请说明理由.
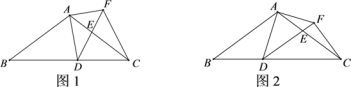
【答案】(1)详见解析;(2)![]() ;(3)点D在BC边上运动 的过程中,存在某个位置,使得DF=CF,此时BD=18.
;(3)点D在BC边上运动 的过程中,存在某个位置,使得DF=CF,此时BD=18.
【解析】
(1)根据两角对应相等的两个三角形相似证明即可;
(2)解直角三角形求出BC,由△ABD∽△DCE,推出![]() =
=![]() ,可得DB=
,可得DB=![]() =
=![]() =
=![]() ,由DE∥AB,推出
,由DE∥AB,推出![]() =
=![]() ,求出AE即可;
,求出AE即可;
(3)点D在BC边上运动的过程中,存在某个位置,使得DF=CF.过点F作FH⊥BC于点H,过点A作AM⊥BC于点M,AN⊥FH于点N,则∠NHA=∠AMH=∠ANH=90°,由△AFN∽△ADM,可得![]() =
=![]() =tan∠ADF=tanB=
=tan∠ADF=tanB=![]() ,推出CH=CM-MH=CM-AN=16-9=7,再利用等腰三角形的性质,求出CD即可解决问题.
,推出CH=CM-MH=CM-AN=16-9=7,再利用等腰三角形的性质,求出CD即可解决问题.
解:(1)∵AB=AC,
∴∠B=∠ACB.
∵∠ADE+∠CDE=∠B+∠BAD,∠ADE=∠B,
∴∠BAD=∠CDE.
∴△ABD∽△DCE.
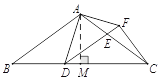
(2)过点A作AM⊥BC于点M.
在Rt△ABM中,设BM=4k,则AM=BM·tanB=4k·![]() =3k.
=3k.
由勾股定理,得:AB2=AM2+BM2,得:
202=(3k)2+(4k)2,解得:k=4.
∵AB=AC,AM⊥BC,
∴BC=2BM=8k=32.
∵DE∥AB,
∴∠BAD=∠ADE.
又∵∠ADE=∠B,∠B=∠ACB,
∴∠BAD=∠ACB.
∵∠ABD=∠CBA,
∴△ABD∽△CBA,
∴![]() =
=![]() ,则DB=
,则DB=![]() =
=![]() =
=![]() .
.
∵DE∥AB,
∴![]() =
=![]() ,
,
∴AE=![]() =
=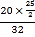 =
=![]() .
.
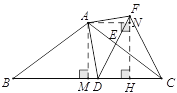
(3)点D在BC边上运动的过程中,存在某个位置,使得DF=CF.
过点F作FH⊥BC于点H,过点A作AM⊥BC于点M,AN⊥FH于点N,则∠NHA=∠AMH=∠ANH=90°.
∴四边形AMHN为矩形.
∴∠MAN=90°,MH=AN.
∵AB=AC,AM⊥BC,
∴BM=CM=![]() BC=
BC=![]() ×32=16.
×32=16.
在Rt△ABM中,由勾股定理,得:AM=![]() =
=![]() =12.
=12.
∵AN⊥FH,AM⊥BC,
∴∠ANF=90°=∠AMD.
∵∠DAF=90°=∠MAN,
∴∠NAF=∠MAD,
∴△AFN∽△ADM.
∴![]() =
=![]() =tan∠ADF=tanB=
=tan∠ADF=tanB=![]() .
.
∴AN=![]() AM=
AM=![]() ×12=9.
×12=9.
∴CH=CM-MH=CM-AN=16-9=7.
当DF=CF时,由点D不与点C重合时,可知△DFC为等腰三角形.
又∵FH⊥DC,
∴CD=2CH=14.
∴BD=BC-CD=32-14=span>18.
∴点D在BC边上运动 的过程中,存在某个位置,使得DF=CF,此时BD=18.

 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案