题目内容
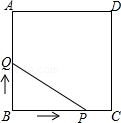
【题目】如图，在三角形ABC中，∠ACB=90°，∠B=50°，将此三角形绕点C沿顺时针方向旋转后得到三角形A′B′C，若点B′恰好落在线段AB上，AC、A′B′交于点O，则∠COA′的度数是（ ）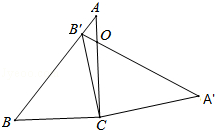 
A.50°
B.60°
C.70°
D.80°
【答案】B
【解析】解：∵在三角形ABC中，∠ACB=90°，∠B=50°， ∴∠A=180°﹣∠ACB﹣∠B=40°．
由旋转的性质可知：
BC=B′C，
∴∠B=∠BB′C=50°．
又∵∠BB′C=∠A+∠ACB′=40°+∠ACB′，
∴∠ACB′=10°，
∴∠COA′=∠AOB′=∠OB′C+∠ACB′=∠B+∠ACB′=60°．
故选B．
由三角形的内角和为180°可得出∠A=40°，由旋转的性质可得出BC=B′C，从而得出∠B=∠BB′C=50°，再依据三角形外角的性质结合角的计算即可得出结论．
练习册系列答案
相关题目
【题目】某公司以每吨
元的价格收购了
吨某种药材，若直接在市场上销售，每吨的售价是
元．该公司决定加工后再出售，相关信息如下表所示：
工艺 | 每天可加工药材的吨数 | 成品率 | 成品售价 （元/吨） |
粗加工 | 14 | 80% | 6000 |
精加工 | 6 | 60% | 11000 |
(注:①成品率80%指加工100吨原料能得到80吨可销售药材；②加工后的废品不产生效益.)
受市场影响，该公司必须在
天内将这批药材加工完毕．
（1）若全部粗加工，可获利_______________________元；
（2）若尽可能多的精加工，剩余的直接在市场上销售，可获利_____________元；
（3）若部分粗加工，部分精加工，恰好天完成，求可获利多少元?
