题目内容
【题目】已知
是最大的负整数，
是多项式
的次数，
是单项式
的系数，且、、分别是点
、
、
在数轴上对应的数．
（1）求、、的值；
（2）若动点
、
同时从、出发沿数轴负方向运动，点的速度是每秒
个单位长度，点的速度是每秒2个单位长度，在数轴上-10处竖立一块档板，运动点碰到档板后马上沿反方向返回，当运动到档板时两点向时停止运动，求当运动几秒后，点碰到点？并求此位置在数轴上表示的数；
（3）在数轴上找一点
，使点到、、三点的距离之和等于13，请直接写出所有点对应的数．（不必说明理由）
【答案】(1)
，
；(2) 当运动9秒后，点Q碰到点P,此位置在数轴上表示的数为0 ；(3) 当点M对应的数为
或
时，点M到A、B、C三点的距离之和等于13
【解析】
(1)根据有理数、多项式和单项式的相关概念，即可求出
、
、
的值；
(2)根据数轴上两点间的距离公式求得路程，再路程、速度、时间的关系进行求解；
(3)分点M在点B的右侧、BC之间、AC之间、点A的左侧四种情况讨论，分别列方程可求得答案．
(1)最大的负整数是
，多项式
的次数是6，单项式
的系数是
,
∴
，；
(2)设当运动t秒后，点P与Q相遇，
依题意得：
，
解得：
，
此时点P的坐标为：
，即原点，
故答数为：当运动9秒后，点Q碰到点P,此位置在数轴上表示的数为0 ；
(3)设点M对应的数为
，使P到A、B、C的距离和等于13，
①当M在点B的右侧，
，
解得：
，因为
，不符合题意，舍去；
②当M在BC之间，
，
解得：
；
③当M在AC之间，
，
解得：
(不符合题意，舍去)；
④当M在点A的左侧，
，
解得：
；
综上，当点M对应的数为或时，点M到A、B、C三点的距离之和等于13．
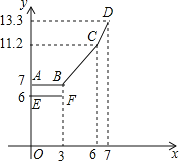
小学夺冠AB卷系列答案
【题目】为缓解油价上涨给出租车待业带来的成本压力，某巿自2018年11月17日起，调整出租车运价，调整方案见下列表格及图象（其中a，b，c为常数）
行驶路程 | 收费标准 | |
调价前 | 调价后 | |
不超过3km的部分 | 起步价6元 | 起步价a 元 |
超过3km不超出6km的部分 | 每公里2.1元 | 每公里b元 |
超出6km的部分 | 每公里c元 | |
设行驶路程xkm时，调价前的运价y1（元），调价后的运价为y2（元）如图，折线ABCD表示y2与x之间的函数关系式，线段EF表示当0≤x≤3时，y1与x的函数关系式，根据图表信息，完成下列各题：
（1）填空：a= ，b= ，c= ．
（2）写出当x＞3时，y1与x的关系，并在上图中画出该函数的图象．
（3）函数y1与y2的图象是否存在交点？若存在，求出交点的坐标，并说明该点的实际意义，若不存在请说明理由．
